Организация как процесс организовывания — одна из основных функций управления. Под функцией управления понимают совокупность повторяющихся управленческих действий, объединенных единством содержания. Поскольку организация (как процесс) служит функцией управления, любое управление представляет собой организационную деятельность, хотя и не сводится к ней.
Управление — особым образом ориентированное воздействие на систему, обеспечивающее придание ей требуемых свойств или состояний. Одним из атрибутов состояния служит структура. Организовать — значит прежде всего создать (или изменить) структуру.
При различиях в подходах к построению систем управления существуют общие закономерности, разработанные в кибернетике. Ответ на поставленный здесь вопрос выглядит так:
система управления = управляющая система (субъект управления) +
+ управляемая система (объект управления).
Базовым классификационным признаком построения систем управления, определяющим облик системы и ее потенциальные возможности, является способ организации контура управления. В соответствии с последним выделяют несколько принципов управления.
Принцип разомкнутого управления. В основе его лежит идея автономного воздействия на систему вне зависимости от условий ее работы. Очевидно, что область практического применения этого принципа предполагает априорную достоверность знания состояния среды и системы на всем интервале ее функционирования. Тогда можно предопределить реакцию системы на рассчитанное воздействие, которое заранее программируется в виде функции независимого переменного времени (рис. 4.1).
Управляющая система Возмущение
Алгоритм Управление
Программы Объект Состояние
Рис.4.1. Принцип разомкнутого управления
Таким образом, если данное воздействие отлично от предполагаемого, немедленно последуют отклонения в характере изменения выходных координат, т. е. система окажется открытой возмущениям. Поэтому данный принцип используется при уверенности в достоверности сведений об условиях работы системы. Например, для организационных систем подобная уверенность допустима при высокой исполнительской дисциплине, когда отданное распоряжение не нуждается в последующем контроле. Иногда такое управление называют директивным. Несомненным достоинством схемы служит простота организации управления.
Принцип разомкнутого управления с компенсацией возмущений. Содержание подхода состоит в стремлении ликвидировать ограниченность первой схемы: нерегулируемое воздействие возмущений на функционирование системы. Возможность компенсации возмущений, а значит, ликвидация недостоверности априорной информации, базируется на доступности возмущений измерениям (рис. 4.2).
Алгоритм Возмущение
компенсации
Компенсирующее
управление
Алгоритм
Программы Объект Состояние
Управляющая Программное
система управление
Рис. 4.2. Принцип компенсационного управления
Измерение возмущений позволяет определять компенсирующее управление, отражающее последствия возмущений. Обычно наряду с корректирующим управлением система подвергается программному воздействию. Однако на практике далеко не всегда удается зафиксировать информацию о внешних возмущениях, не говоря о контроле отклонений параметров системы или неожиданных структурных изменениях. При наличии информации о возмущениях принцип их компенсации путем введения компенсирующего управления представляет практический интерес.
Принцип замкнутого управления. Рассмотренные принципы относятся к классу разомкнутых контуров управления: величина управления не зависит от поведения объекта, а представляет собой функцию времени или возмущения. Класс замкнутых контуров управления образуют системы с отрицательной обратной связью, воплощающие базовый принцип кибернетики. В таких системах заранее программируется не входное воздействие, а требуемое состояние системы, т. е. следствие
воздействий на объект, в т. ч. управления. Следовательно, возможна ситуация, когда возмущение позитивно воздействует на динамику системы, если приближает ее состояние к желаемому. Для реализации принципа априорно находится программный закон изменения состояния системы во времени , а задача системы формулируется как обеспечение приближения действительного состояния к желаемому (рис. 4.3). Решение этой задачи достигается определением разности между желаемым и действительным состояниями: 
с(t) = с
(t) - с(t). Данная разность используется для управления, призванного свести к минимуму обнаруженное рассогласование. Тем самым обеспечивается приближение регулируемой координаты к программной функции вне зависимости от причин, вызвавших появление разности, будь то возмущения различного происхождения или ошибки регулирования. Качество управления сказывается на характере переходного процесса и установившейся ошибке — несовпадении программного и действительного конечного состояния.
возмущение
с(t)
Объект
управление
Объект
управления
В зависимости от входного сигнала в теории управления различают:
- системы программного регулирования (рассматриваемый случай);
- » системы стабилизации, когда с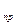(t) = 0;
- » системы слежения, когда входной сигнал априорно неизвестен.
Эта детализация никак не сказывается на реализации принципа замкнутого управления, но вносит специфику в технику построения системы.
Широкое распространение этого принципа в естественных и искусственных системах объясняется продуктивностью взаимодействия элементов системы управления: задача управления эффективно решается на концептуальном уровне благодаря отрицательной обратной связи.
Выше рассмотрен случай программирования изменения во времени состояния системы с(t), что, согласно введенной терминологии, означает предварительный расчет траектории в пространстве состояний. Этот расчет выполняется при учете двух требований: траектория должна проходить через цель и удовлетворять экстремуму критерия качества, т.е. быть оптимальной.
В формализованных динамических системах для отыскания подобной траектории привлекается аппарат вариационного исчисления или его современные модификации6 принцип максимума Л.Понтрягина, динамическое программирование Р.Беллмана. Когда задача сводится к поиску неизвестных параметров (коэффициентов) системы, для ее решения привлекаются методы математического программирования – требуется отыскать экстремум функции качества (показателя) в пространстве параметров. Чтобы справиться с плохо формализуемыми проблемами, остается уповать на эвристические решения, основанные на футурологических прогнозах, или на результаты имитационного математического моделирования. Точность подобных решений оценить сложно.
Возвратимся к задаче программирования. Если существует способ программной траектории для формализованных задач, естественно потребовать от системы управления, чтобы она довольствовалась целеуказанием, а программное изменение состояния система находила непосредственно в процессе управления (управление в этом случае называется терминальным). Такая организация системы, конечно, усложняет алгоритм управления, но позволяет свести к минимуму исходную информацию, а значит. Делает управление более оперативным. Подобная задача в 1960-х гг. была теоретически решена профессором Е.Горбатовым для управления движением баллистических ракет и космических аппаратов.
При постановке и решении задачи оптимального управления следует учитывать следующее принципиальное обстоятельство. Строго говоря, только тогда можно выбрать оптимальное поведение системы, когда достоверно известны поведение изучаемого объекта на всем интервале управления и условия, в которых происходит движение. Оптимальные решения могут быть получены и при выполнении других, дополнительных допущений, но дело как раз в том, что каждый случай следует оговаривать особо, и решение будет справедливо «с точностью до условий».
Проиллюстрируем сформулированное положение на примере поведения бегуна, стремящегося достичь высокого результата. Если речь идет о короткой дистанции (100 или 200 м), то подготовленный спортсмен ставит целью обеспечить максимальную скорость в каждый момент времени. При беге на более длинные дистанции успех спортсмена определяется его умением правильно распределять силы на трассе, а для этого надо отчетливо представлять себе свои возможности, рельеф маршрута и силы соперников. Ни о какой максимальной скорости в каждый момент не может идти и речи в условиях ограниченных ресурсов.
Очевидно, что приведенное ограничение выполняется только в рамках детерминированной постановки задачи, т.е. когда априорно все достоверно известно. Такие условия оказываются чрезмерными для реальных задач — прокрустово ложе детерминизма не соответствует действительным условиям функционирования системы. Априорность нашего знания чрезвычайно сомнительна в отношении как самой системы, так и среды и ее взаимодействия с тем или иным объектом. Достоверность априорных сведений тем меньше, чем сложнее система, что не добавляет оптимизма исследователям, проводящим процедуру синтеза.
Подобная неопределенность привела к появлению целого направления в теории управления, базирующегося на учете стохастических условий существования системы. Самые конструктивные результаты были получены при разработке принципов адаптивных и самонастраивающихся систем.
Адаптивные системы позволяют справляться с неопределенностью путем получения и использования дополнительной информации о состоянии объекта и его взаимодействии со средой в процессе управления с последующей перестройкой структуры системы и изменением ее параметров при отклонении условий работы от априорно известных (рис. 4.4). При этом, как правило, цель трансформаций состоит в приближении характеристик системы к априорным, использовавшимся при синтезе управления. Таким образом, адаптация ориентирована на сохранение гомеостаза системы в условиях возмущений.
возмущение
Состояние
Объект
Управление
Информация об объекте
Алгоритмы
управления
Сведения о процессах
Коррекция управления
управления
Алгоритм
адаптации
Управляющая
система
Рис.4.4. Адаптивная система
Одна из сложнейших конструктивных составляющих этой задачи — получение сведений о состоянии среды, без чего затруднительно проводить адаптацию.
Примером успешного получения информации о состоянии среды может быть изобретение трубки Пито, которой снабжены практически все летательные аппараты. Трубка позволяет измерить скоростной напор — важнейшую характеристику, от которой непосредственно зависят все аэродинамические силы. Результаты измерения используются для настройки автопилота. Аналогичную роль в общественной жизни играют социологические опросы, позволяющие корректировать решения внутри- и внешнеполитических проблем.
Эффективным приемом изучения динамики объекта управления является метод дуального управления, некогда предложенный А. Фельдбаумом. Суть метода в том, что на объект наряду с командами управления подаются специальные тестирующие сигналы, реакция на которые для априорной модели заранее установлена. По отклонению реакции объекта от эталонной судят о взаимодействии модели с внешней средой.
Подобный прием использовался в русской контрразведке во время Первой мировой войны для выявления шпиона. Выделялся круг сотрудников, подозреваемых в предательстве, и каждому из этого круга «доверялась» важная, но ложная информация, имеющая уникальный характер. Наблюдалась реакция противника, по которой и идентифицировался изменник.
От адаптивных систем отличают класс самонастраивающихся систем. Последние в процессе адаптации настраиваются. Однако на принятом уровне общности структура самонастраивающейся системы аналогична структуре адаптивной системы (см. рис. 4.4).
Относительно процессов адаптации и самонастройки систем можно отметить, что их возможность в конкретных случаях в основном определяется назначением системы и ее техническим воплощением. Подобная теория систем изобилует иллюстрациями, но, как представляется, не содержит обобщающих достижений.
Другой путь преодоления недостаточности априорных данных о процессе управления заключается в совмещении процесса управления с процедурой синтеза. Традиционно алгоритм управления есть результат синтеза, базирующийся на допущении детерминированного описания модели движения. Но очевидно, что отклонения в движении принятой модели сказываются на точности достижения цели и на качестве процессов, т. е. приводят к отклонению от экстремума критерия. Отсюда следует, что строить управление нужно как терминальное, рассчитывая траекторию в реальном времени и обновляя сведения о модели объекта и условиях движения. Конечно, и в данном случае необходимо экстраполировать условия движения на весь оставшийся интервал управления, но по мере приближения к цели точность экстраполяции возрастает, а значит, повышается качество управления.
В этом видна аналогия с действиями правительства, которое не в состоянии выполнять плановые задания, например бюджетные. Условия функционирования экономики меняются нерасчетным образом, с нарушением прогнозов, поэтому приходится постоянно корректировать намеченный план в стремлении достичь итоговых показателей, в частности производить секвестр. Отклонения от априорных предположений могут быть столь велики, что имеющимися ресурсами и принимаемыми мерами управления уже нельзя обеспечить выполнение цели. Тогда приходится «приближать» цель, размещая ее внутри новой области достижимости. Отметим, что описанная схема справедлива только для устойчивой системы. Низкое качество организации управления может привести вообще к дестабилизации и, как следствие, к разрушению всей системы.
Наконец, следует остановиться еще на одном принципе управления, лежащем в основе развитой теории исследования операций.
Принцип однократного управления. Широкий круг практически значимых задач состоит из необходимости осуществить однократный акт управления, а именно — принять некоторое решение, последствия которого сказываются длительное время. Разумеется, и традиционное управление можно интерпретировать как последовательность разовых решений. Здесь мы вновь сталкиваемся с проблемой дискретности и непрерывности, граница между которыми так же размыта, как и между статическими и динамическими системами. Однако различие все-таки существует: в классической теории управления исходят из того, что воздействие на систему есть процесс, функция времени или параметров состояния, а не однократная процедура.
Другой отличительной особенностью исследования операций является то, что эта наука оперирует с управлениями-константами, параметрами системы. Тогда, если в динамических задачах в качестве критерия используется математическая конструкция — функционал, оценивающий движение системы, то в исследовании операций критерий имеет вид функции, заданной на множество исследуемых параметров системы.
Область практических задач, охватываемая исследованием операций, весьма обширна и включает мероприятия по распределению ресурсов, выбору маршрутов, составлению планов, управлению запасами, очередями в задачах массового обслуживания и др. При решении соответствующих задач привлекается изложенная выше методология их описания с учетом категорий модели, состояния, цели, критерия, управления. Так же формулируется и решается проблема оптимизации, состоящая в нахождении экстремума критериальной функции в пространстве параметров. Задачи решаются как в детерминированной, так и в стохастической постановке.
Так как процедура оперирования с константами существенно проще, чем действия с функциями, то теория исследования операций оказалась продвинутой дальше, нежели общая теория систем, в частности теория управления динамическими системами. Исследование операций предлагает больший арсенал математических средств, порой весьма утонченных, для решения широкого круга практически значимых задач. Вся совокупность математических методов, обслуживающих исследование операций, получила название математического программирования. Так, в рамках исследования операций развивается теория принятия решений — чрезвычайно актуальное направление.
Теория принятия решений по сути представляет собой процедуру оптимизации условий детального описания векторного критерия и особенностей установления его экстремального значения. Так, для постановки задачи характерен критерий, состоящий из нескольких составляющих, т. е. многокритериальная задача.
Для подчеркивания субъективизма критерия и процесса принятия решения в рассмотрение вводится лицо, принимающее решение (ЛПР), обладающее индивидуальным взглядом на проблему. При изучении решений формальными методами это проявляется через систему предпочтений при оценке той или иной составляющей критерия.
Как правило, для принятия решения ЛПР получает несколько вариантов действий, каждый из которых подвергается оценке. Такой подход максимально приближен к реальным условиям действий ответственного субъекта в организационной системе при выборе одного из вариантов, подготовленных аппаратом. За каждым из них стоит проработка (аналитическое или имитационное математическое моделирование) возможного хода развития событий с анализом конечных результатов — сценарий. Для удобства принятия ответственных решений организуются ситуационные комнаты, оборудованные наглядными средствами отображения сценариев на дисплеях или экранах. Для обслуживания таких образований привлекаются специалисты (операционалисты), владеющие не только математическими методами анализа ситуаций и подготовки принятия решений, но и предметной областью.
Понятно, что результатом применения к объекту теории исследования операций, в частности теории принятия решений, является оптимальный план действий. Следовательно, на вход некоторого блока, «начиненного» оптимизационным алгоритмом и построенного с применением соответствующего метода математического программирования к модели ситуации, подается информация: начальное состояние, цель, критерий качества, перечень варьируемых параметров, ограничения. (Модель системы используется при построении алгоритма.) Выход блока и есть искомый план. С точки зрения кибернетики такое построение классифицируется как разомкнутый контур управления, поскольку выходная информация не влияет на входной сигнал.
Принципиально можно расширить рассмотренный подход на случай замкнутого управления. Для этого необходимо организовать итерационный процесс во времени: после реализации плана ввести новое состояние системы в качестве начального условия и повторить цикл. Если позволяет задача, можно сократить плановый период за счет приближения цели к начальному состоянию системы. Тогда просматривается аналогия предлагаемых действий с рассмотренной выше итерационной процедурой терминального управления, также базирующейся на периодическом обновлении исходной информации. Более того, динамическую задачу, оперирующую с процессами, можно свести к аппроксимации функций функциональными рядами. При этом варьируемыми переменными уже будут параметры таких рядов, а значит, применим аппарат теории исследования операций. (Так делают в теории вероятностей, когда описывают случайные процессы каноническим разложением.)
Изложенная методология уже находит применение в теории искусственного интеллекта при синтезе ситуационного управления.
Следует указать на опасность, связанную с практическим применением теории решений недостаточно компетентными в теории систем лицами. Так, часто в организационных системах (госучреждениях, фирмах, финансовых организациях) принятие решения абсолютизируют и сводят к оперированию многочисленными показателями и оптимальному осуществлению разового управленческого акта. При этом выпадают из поля зрения последствия произведенного действия для системы; забывают, что управляют не критерием, а системой, не учитывая многостадийный замкнутый процесс — от системы к ее состоянию, далее через показатели к решению и вновь к системе. Конечно, на этом долгом пути делается множество ошибок, объективных и субъективных, которых уже достаточно для серьезного отклонения от плановых результатов. Итак, рассмотренные принципы управления предоставляют исследователю чрезвычайно широкие возможности для построения систем управления. С учетом этих принципов рассмотрим методы управления применительно к менеджменту.
Поможем написать любую работу на аналогичную тему