Билет 1 по квантовой механике

Частица с массой  и энергией  падает на прямоугольную потенциальную ступень:      

          а) определить коэффициенты отражения и прозрачности для случая, когда ;

          б) определить коэффициент отражения для случая, когда .

Решение.

          а) Рассмотрим случай, когда , где требуется найти коэффициенты отражения и прозрачности, которые определяются по формулам соответственно:

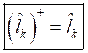 и .

          В этом случае стационарное уравнение Шредингера для областей I и II перепишется в следующем виде:

I:        ,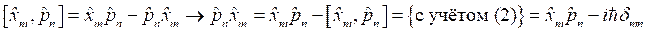

II:       .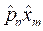

          Решением дифференциального уравнения (1) является волновая функция . Подставляя это решение в (1) получаем:

,

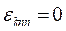а значит для области I волновая функция примет следующий вид:

.

          Решением дифференциального уравнения (2) является волновая функция . Подставляя это решение в (2) получаем:

,

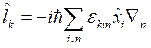а значит для области II волновая функция примет следующий вид:

.

          Так как в области II присутствует только волна, прошедшая через барьер  и распространяющаяся в положительном направлении оси ОХ, то необходимо положить равным нулю коэффициент . Вследствие этого получим:

I:                               и         

II:                                          и          .

          С учётом граничных условий получим систему коэффициентов:

.

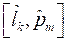          Отсюда найдём отношение коэффициентов  и :

.

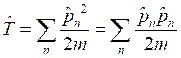          Подставляем  во второе уравнение и находим :

.

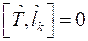          Находим коэффициент отражения: 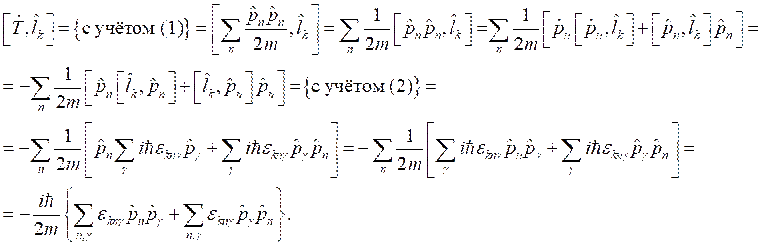, а коэффициент прозрачности:

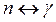
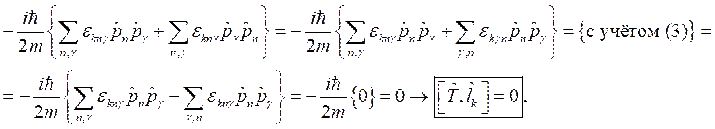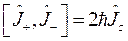          Таким образом:  и , где 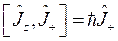 - что и требовалось найти.