Нужна помощь в написании работы?
Показать, что произвольный оператор может быть представлен в виде суммы эрмитовой и антиэрмитовой частей.
Решение.
Представим некий оператор 
в следующем виде:
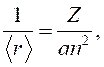, где символ «
» - эрмитово сопряжение.
Далее отдельно сформируем следующие част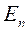и:
и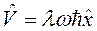 
.
Чтобы утверждать, что 
и 
- требуемые части, необходимо проверить выполнение условия эрмитовости операторов, а именно: 
и 
. Таким образом:
;
.
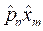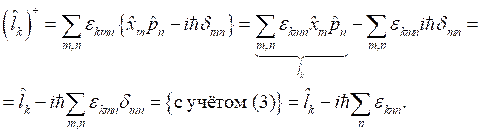Т.о. 
, где и - эрмитова и антиэрмитова части соответственно.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость