Учитывая, что операторы координаты и импульса эрмитовы показать, что оператор декартовой компоненты орбитального момента тоже является эрмитовым.
Решение.
По свойству эрмитовости для операторов координаты и импульса:
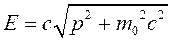(1).
Коммутатор операторов компоненты координаты и компоненты импульса:
(2).
Правило работы с дельта-символом Кронекера:
(3).
Оператор декартовой компоненты орбитального момента:
,
а с учётом того, что 
, получаем: 
.
Требуется показать выполнение следующего равенства:
.
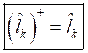Произведём сопряжение оператора декартовой компоненты орбитального момента и далее преобразуем полученное выражение:
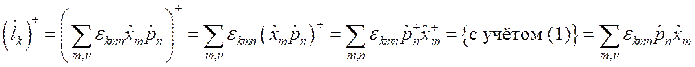(4).
Рассмотрим следующий коммутатор и его преобразование:
.
Далее подставим выражение для 
в выражение (4) и проведём преобразования:
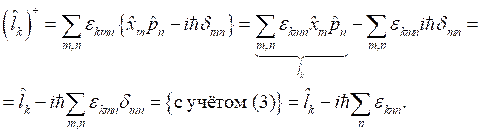
Так как два индекса равны, то 
, что делает вычитаемое равным нулю, а значит:
, что и требовалось показать.
Поможем написать любую работу на аналогичную тему