Анализ программ и учебников.

Рассмотрим представление темы «Симметрические многочлены» в основных комплектах  школьных учебников авторов Виленкина Н.Я., Дорофеева Г.В., Башмакова М.И. Колягина Ю.М.Мордковича А.Г.. Для начала отметим, что программа по математике для обычных классов общеобразовательной школы не предусматривает введения понятия симметрических многочленов, а в программе для классов с углубленным изучением математики этот вопрос стоит  в явном виде.

  В учебнике Виленкина Н.Я. «Алгебра и начала анализа»11 класс для школ и классов с углубленным изучением математики теория симметрических многочленов и ее применение рассматривается достаточно подробно. После введения понятия многочлена от нескольких переменных автор вводит понятие симметрического многочлена сначала на примере многочлена от двух переменных, а затем дает точное определение «Многочлен  называется симметрическим, если при любой перестановке входящих в него букв получается тождественно равный ему многочлен». Дается  общий способ получения симметрических многочленов:  «Выражение  при любой перестановке буков   переходит в тождественно равное ему выражение (отличающее от исходного лишь порядком следования множителей). Поэтому если раскрыть скобки, то коэффициенты при степенях , будут симметрические многочлены от  переменных » и вводится понятие основных симметрических многочленов и степенных сумм. Рассмотрена основная теорема о  симметрических многочленах с доказательством. Доказательство проведено методом математической индукции  при помощи вспомогательной теоремы: «Любая степенная сумма  может быть представлена в виде многочленов от 1=х + y  и 2 =xy». Приведено доказательство теоремы для случая .

Задания, предлагаемые автором, сводятся к применению теории для разложения многочленов на множители решению уравнений четвертой степени.

Затем автор возвращается к понятию симметрического многочлена при изучении темы «Системы уравнений и неравенств» в пункте «Метод замены переменных. Системы симметрических уравнений». Этот пункт отмечен звездочкой, что говорит о том, что излагаемый материал несколько больше по объему предусмотренного программой углубленного изучения математики. В данном пункте приведены примеры как решения систем симметрических многочленов, так и применение теории симметрических многочленов для решения иррациональных уравнений.

Автором предложены задания только на решения систем уравнений.

В учебнике Мордковича А.Г «Алгебра углубленное изучение» для 9 класса сначала вводится понятие симметрических выражений: «Выражение называется симметрическим, если оно сохраняет свой вид при одновременной замене  на , а  на  », а на основании  этого определения вводится понятие симметрического уравнения. Дано понятие основных симметрических многочленов и неявно сформулирована основная теорема о симметрических многочленах (без доказательства). Сформулировано определение системы симметрических многочленов с двумя неизвестными  и идея решения.

В учебнике Башмакова М.И. «Алгебра и начала анализа» для 10-11 классов общеобразовательных учреждений в главе 6 «Уравнения и неравенства» отдельным пунктом рассмотрены системы симметрических уравнений. Четко сформулировано определение симметрической системы. Решение симметрических систем уравнений вида 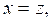 основывается на теореме обратной к теореме Виета. Для нахождения корней такой системы необходимо найти корни уравнения . «Решение других систем основываются на том, что любое симметрическое относительно   и выражение можно выразить через новые переменные u=х + y  и v=xy».

В учебнике Колягина Ю.М. «Алгебра и начала анализа» для 10 класса общеобразовательных учреждений данная теория рассмотрена в пункте «Решения систем уравнений различными способами». Понятие симметрического многочлена не вводится. Решение симметрических уравнений разобраны на конкретных примерах и основываются на применение теоремы Виета.

Шабунин М.И. в учебнике «Алгебра. Начала математического анализа» для 10 класса профильного уровня в главе 8 отдельными пунктами выделяет симметрические системы  уравнений  с двумя и тремя неизвестными. В пункте «Симметрические системы с двумя неизвестными», автор четко формулирует определение систем симметрических уравнении основываясь на определение симметрических многочленов и решение сводится к применению теоремы Виета. Вводится понятие простейших симметрических многочленов (х + y; xy) и  формулируется основная теорема без доказательства. Приведены примеры нахождения симметрических сумм  при n=2,3,4,5. Рассмотрены примеры нахождения действительных решений систем уравнений высших степеней. Аналогичным образом рассмотрены системы уравнений с тремя неизвестными.

Дорофеев Г.В.  в учебнике «Алгебра и начала анализа» 10 класс для общеобразовательных учреждений подробно излагает понятие симметрического многочлена. Определение формулируется после приведения конкретных примеров и для n переменных: «…многочлен от нескольких переменных называют симметрическим, если он не меняется при перенумерации переменных». Вводится понятие элементарных симметрических многочленов, приведены примеры элементарных симметрических многочленов с 4 переменными. Основная теорема о симметрических многочленах сформулирована не четко и доказательство не приводится. Затем автор подробно излагает теорему Виета для многочленов выше второй степени формулируя ее сначала для многочлена третей степени со старшим коэффициентом 1. Приведены разнообразные примеры применения теории симметрических многочленов.