Лекция 1: Симметрические многочлены от двух переменных. Симметрические многочлены от трех переменных.
Симметрические многочлены от двух переменных
Определение. Многочлен f (х,у) называют симметрическим, если он не изменяется при замене x на y,а y на x.
Многочлен ![]() - симметрический. Напротив многочлен
- симметрический. Напротив многочлен ![]() не является симметрическим: при замене
не является симметрическим: при замене ![]() на
на![]() , а
, а ![]() на
на![]() он превращается в многочлен
он превращается в многочлен![]() , который не совпадает с первоначальным.
, который не совпадает с первоначальным.
Приведем примеры симметрических многочленов. Как известно из арифметики, сумма двух чисел не меняется при перестановке слагаемых, т.е.
![]()
для любых чисел ![]() и
и ![]() . Это равенство показывает, что многочлен
. Это равенство показывает, что многочлен ![]() является симметрическим.
является симметрическим.
Точно так же из закона коммутативности умножения
![]()
Следует, что произведение ![]() является симметрическим многочленом.
является симметрическим многочленом.
Рассмотренные примеры симметрических многочленов являются самыми простыми. Их называют элементарными симметрическими многочленами от ![]() и
и ![]() . Для них используется специальное обозначение:
. Для них используется специальное обозначение:
![]() ,
, ![]()
Кроме ![]() и
и ![]() ,часто встречатюся так называемые степенные суммы, т.е. многочлены
,часто встречатюся так называемые степенные суммы, т.е. многочлены ![]() Принято обозначать многочлен
Принято обозначать многочлен ![]() через
через ![]() . Таким образом,
. Таким образом,
![]() ,
,
![]()
![]()
![]() ,
,
…………….
Существует простой прием, позволяющий получать симметрические многочлены. Возьмем любой (вообще говоря, не симметрический) многочлен от ![]() 1 и
1 и ![]() 2 и подставим в него вместо
2 и подставим в него вместо ![]() 1 и
1 и ![]() 2 их выражения через x и у. Ясно, что при этом мы получим симметрический многочлен от x и у
2 их выражения через x и у. Ясно, что при этом мы получим симметрический многочлен от x и у
Если взять любой многочлен от ![]() 1
и
1
и ![]() 2 и подставить в него вместо
2 и подставить в него вместо![]() 1
и
1
и ![]() 2 их выражение
2 их выражение ![]() 1
= х+у,
1
= х+у, ![]() 2=ху, то получится симметрический многочлен f (х, у).
2=ху, то получится симметрический многочлен f (х, у).
Теорема. Любой симметрический многочлен от x и y можно представить в виде многочлена от ![]() 1=х + y и
1=х + y и ![]() 2 =xy.
2 =xy.
Доказательство: Сначала докажем теорему не для любых симметрических многочленов, а лишь для степенных сумм. Иными словами, мы установим, что каждую степенную сумму sn=xn+yn можно представить в виде многочлена от ![]() и
и ![]() .
.
С этой целью умножим обе части равенства
sk-1= хk-1
+ ук-1 на ![]() 1= x+y.
1= x+y.
Получим:
![]() 1sk-1=(х+ y)(хк-1+yк-1)=хк+ хyk-1+x к-1у+уk= хк + yk + ху (хk-2 + уk-2) =
1sk-1=(х+ y)(хк-1+yк-1)=хк+ хyk-1+x к-1у+уk= хк + yk + ху (хk-2 + уk-2) =
= sk
+ ![]() k+
k+![]() 2sk-2
2sk-2
Таким образом,
sk=![]() 1sk-1-
1sk-1-![]() 2sk-2 (1)
2sk-2 (1)
Докажем равенство (1) методом математической индукции.
При к=1 s1=x+y=![]() формула верна. Предположим, что она верна при k=n-1 т.е. sn выражается через
формула верна. Предположим, что она верна при k=n-1 т.е. sn выражается через ![]() и
и
![]() , проверим выполнимость формулы при k=n sn=
, проверим выполнимость формулы при k=n sn=![]() 1sn-1-
1sn-1-![]() 2sn-2 , по предположению sn-1,sn-2 выражаются через
2sn-2 , по предположению sn-1,sn-2 выражаются через![]() и
и
![]() , следовательно и sn
выражаются через
, следовательно и sn
выражаются через![]() и
и
![]() .Условия теоремы математической индукции выполняются, значит sk=
.Условия теоремы математической индукции выполняются, значит sk=![]() 1sk-1-
1sk-1-![]() 2sk-2 верна для любого k.
2sk-2 верна для любого k.
Любой симметрический многочлен от х и y содержит (после приведения подобных членов) слагаемые двух видов.
Во-первых, могут встречаться одночлены, в которые х и у входят в одинаковых степенях, т.е. одночлены вида ахkуk. Ясно, что
ахkуk = а (ху)k= а![]() k2,
k2,
т. е. одночлены этого вида непосредственно выражаются через ![]() .
.
Во-вторых, могут встретиться одночлены, имеющие разные степени относительно х и у, т. е, одночлены вида bхkуl, где k.![]() l. Ясно, что вместе с одночленом bхkуl симметрический многочлен содержит также и одночлен bхlуk получаемый из bхkуl перестановкой букв х и у. Другими словами, в симметрический многочлен входит двучлен вида b(хkуl + хlуk)
l. Ясно, что вместе с одночленом bхkуl симметрический многочлен содержит также и одночлен bхlуk получаемый из bхkуl перестановкой букв х и у. Другими словами, в симметрический многочлен входит двучлен вида b(хkуl + хlуk)
Предполагая для определенности l>k, можно переписать этот двучлен следующим образом: b(хkуl + хlуk)=bxkyk(yl-k+xl-k)=b![]() k2sl-k.. А т. к. по доказанному степенная сумма sl-k представляется в виде многочлена от
k2sl-k.. А т. к. по доказанному степенная сумма sl-k представляется в виде многочлена от![]() 1 и
1 и ![]() 2, то и рассматриваемый двучлен выражается через
2, то и рассматриваемый двучлен выражается через ![]() 1 и
1 и ![]() 2.
2.
Итак, каждый симметрический многочлен представляется в виде суммы одночлена вида ахkуk и двучлена вида ![]() , каждый из которых выражается через
, каждый из которых выражается через ![]() 1 и
1 и ![]() 2 . Следовательно, любой симметрический многочлен представляется в виде многочлена от
2 . Следовательно, любой симметрический многочлен представляется в виде многочлена от ![]() 1 и
1 и ![]() 2. Теорема полностью доказана.
2. Теорема полностью доказана.
Симметрические многочлены от трех переменных
Мы рассмотрели симметрические многочлены от двух переменных х, у, т. е. многочлены, которые не меняются при перестановке местами х и у. В многочлене от трех переменных х, у, z таких перестановок можно сделать не одну, а три: можно поменять местами х и у или х и z, или, наконец, у и z.
Определение. Многочлен f (х, у, z) называется симметрическим, если при любой перестановке переменных он остается неизменным .
Условие симметричности многочлена f (х, у, z) записывается следующим образом:
f (х, у, z)=f(у, х, z)=f(z, y, х)=f(х, z, у).
Из коммутативности сложения вытекает, что симметричным является многочлен x+y+z, а из коммутативности умножения следует симметричность многочлена xyz.
Симметричны и степенные суммы, т. е. многочлены, вида
![]() .
.
Вот еще примеры симметрического многочлена от трех переменных:
ху +yz+xz,
![]() ,
,
![]()
![]()
Напротив, многочлен х2z + у2z не является симметрическим. Правда, при перестановке переменных х и y
он не меняется: х2z + у2х = у2z + х2z.Но перестановка переменных x и z меняет вид этого многочлена – он переходит в многочлен ![]()
Наиболее простыми являются симметрические многочлены ![]() ,
, ![]() ,
, ![]() .
.
Их называют элементарными симметрическими многочленами
от трех переменных x,y,z и обозначают через ![]()
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Заметим, что многочлен ![]() - многочлен первой степени,
- многочлен первой степени,![]() - второй степени и
- второй степени и ![]() - многочлен третий степени.
- многочлен третий степени.
Как и в случае двух переменных, можно построить симметрические многочлены от трех переменных. Возьмем любой многочлен от переменных, ![]() и заменим в нем
и заменим в нем ![]() на x+y+z,
на x+y+z, ![]() -на xy+xz+yz и
-на xy+xz+yz и ![]() - на xyz. В результате мы получим многочлен, симметрично зависящий от х, у, z.
- на xyz. В результате мы получим многочлен, симметрично зависящий от х, у, z.
Теорема. Любой симметрический многочлен от х, у, z можно представить в виде многочлена от ![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.
Доказательство основной теоремы о симметрических многочленах от трех переменных несколько сложнее, чем для случая двух переменных, поэтому опустим его. (Приложение 3).
Лекция 2. Определение симметрических многочлена от m переменных. Свойства симметрических многочленов. Основная теорема о симметрических многочленах
Определение. Многочлен от m переменных называется симметрическим многочленом, если он не изменяется при любой перестановке переменных.
Пример. Многочлен f(x1,x2,x3)=x12+x22+x32 является симметрическим т.к. f(x2,x1,x3)=x23+x13+x33= f(x3,x2,x1)= f(x1,x2,x3)
Многочлен g(x1,x2,x3)=3x13+x23+3x33 симметрическим не является т.к. g(x2,x1,x3)=3x23+x13+3x33 ![]() g(x1,x2,x3)
g(x1,x2,x3)
Пример. Многочлен x12+…+xm2+x1+x2+…+xmпереходит в себя при любой подстановке элементов x1,…,xm.
Определение. Элементарными симметрическими многочленами от x1,…,xm называются многочлены
s1=x1+x2+…+xm;
s2=x1x2+x1x3+…+xm-1xm;
s3=x1x2 x3+…+xm-2xm-1xm;
………………………………
sm=x1x2…xm.
Элементарные симметрические многочлены получаются, если рассмотреть многочлена j=(z-x1)(z-x2)…(z-xm), который равен многочлену
zm-(x1+x2+…+xm)zm-1+(x1x2+…+xm-1xm)zm-2+…+(-1)mx 1...xm.
Таким образом, j=zm-s1zm-1+s2zm-2-…+(-1)msm.
Свойства симметрических многочленов
10 Сумма, разность, произведение симметрических многочленов является симметрическим многочленом, т.е. множество симметрических многочленов является кольцом.
20 Всякий симметрический многочлен можно представить в виде суммы однородных многочленов.
30 Если одночлен axna1 xna2…xnan входит в симметрический многочлен, то в этот симметрический многочлен входят и одночлены, полученные из данного любой перестановкой переменных.
40 Показатели степеней переменных в высшем члене симметрического многочлена образуют не возрастающую последовательность.
50 Пусть ax1k1x2k2…xmkm- высший член ненулевого симметрического многочлена f(x1,…,xm) ÎK.Тогда высшие члены многочленов f(x1,…,xm) и as1k1-k2s2k2-k3…smkm совпадают.
60 Убывающая цепочка ненулевых симметрических многочленов кольца многочленов K не может быть бесконечной.
Доказательство некоторых свойств можно рассмотреть на практическом занятие или предложить учащимся это выполнить самостоятельно.
Основная теорема о симметрических многочленах
Теорема. Всякий симметрический многочлен из кольца многочленов K можно представить в виде многочлена над K от элементарных симметрических многочленов s1,…,sm, т.е. для любого f(x1,…,xm)Î K существует такой многочлен g(x1,…,xm) Î K, что f(x1,…,xm)= g(s1(x1,…,xm),…,sm(x1,…,xm))
Доказательство. Пусть многочлена f(x1,…,xm) -не нулевой симметрический многочлен над K и a0x1k1x2k2…xmkm -его высший член. Многочлен (1) f1= f- a0sk1-k2…smkm -симметрический, как разность симметрических многочленов, причем, по свойству 50, f > f1. Пусть a1x1l1 …xm lm - высший член многочлена f1. Аналогично, многочлен (2) f2= f1- a1s l1- l2…sm lm является симметрическим, причем f1> f2 и т.д. В результате получается убывающая цепочка симметрических многочленов f> f1> f2> …..По свойству 60, эта цепочка не может быть бесконечной. Предположим, что она обрывается на (s+1)-м шаге, т.е. (s+1) fs+1= fs- assn1-n2…smnm =0. Складывая почленно равенства (1),(2),…,(s+1), получим
f= a0sk1-k2…smkm + a1s l1- l2…sm lm + …+ assn1-n2…smnm .
Это равенство дает искомое представление симметрического многочлена f в виде многочлена над K от элементарных симметрических многочленов s1,…,sm.
Следствие. Пусть j = zm+a1zm-1+…+am- многочлен над числовым кольцом K и j = (z-c1)(z-c2)…(z-cm), где c1,…,cmÎC. Если f(x1,…,xm)- симметрический многочлен от x1,…,xm с коэффициентами из K, то f(с1,…,сm)Î K.
Доказательство: Из равенства
(z-c1)(z-c2)… (z-cm) = zm+a1zm-1+ a2zm-2+…+am
вытекают следующие формулы (формулы Виета), выражающие связь между корнями и коэффициентами многочлена:
с1+…+сm= -a1;
c1c2+…+cm-1cm= a2;
…………………….
c1c2…cm= (-1)mam.
Эти равенства можно записать в виде
s1( с1,…,сm) = -a1;
s2( с1,…,сm) = a2;
……………….. (1)
sm ( с1,…,сm) = (-1)mam. ;
В силу основной теоремы о симметрических многочленах симметрический многочлен f из K можно представить в виде многочлена g от элементарных симметрических многочленов s1,…,sm с коэффициентами из K, т.е.
f(x1,…,xm)= g(s1(x1,…,xm),…,sm(x1,…,xm)). (2)
Полагая в равенстве (2) x1=c1,…,xm=cm и учитывая равенства (1), получим
f(c1,…,cm)= g(-a1, a2,…, (-1)mam) (3)
Кроме того, gÎ K и a1,…,amÎ K, следовательно, f(c1,…,cm) Î K.
Лекция 3: Решение систем уравнений от двух переменных
Теорема 1. Пусть ![]() и
и ![]() - два произвольных числа. Квадратное уравнение
- два произвольных числа. Квадратное уравнение
![]()
![]()
и система уравнений
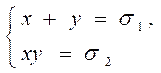
![]()
связанны друг с другом следующим образом: если z1, z2
корни квадратного уравнения ![]() , то система имеет два решения
, то система имеет два решения
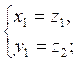
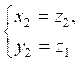
и других решений не имеет; обратно, если x=a,
y=b
– решение системы![]() , то числа a и b является корнями уравнения
, то числа a и b является корнями уравнения ![]() .
.
Доказательство. Если ![]() и
и ![]() - корни квадратного уравнения
- корни квадратного уравнения![]() , то по формулам Виета
, то по формулам Виета
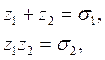
т.е. числа
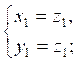
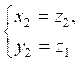
![]() является решениями системы
является решениями системы ![]() .
.
Пусть ![]()
![]() -
решение системы
-
решение системы ![]()
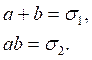
Тогда имеем:
![]() .
.
Но это означает, что числа a и b являются корнями квадратного уравнения ![]() . Теорема доказана.
. Теорема доказана.
Система двух уравнений с двумя неизвестными, состоящая из несимметрических уравнений, может быть сведена к симметричной системе введением новых (вспомогательных) неизвестных. Например, если в системе
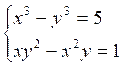
заменить неизвестное у новым неизвестным z=-y придем к системе
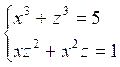
левые части, которой симметрично зависят от x и y.
Иногда нужная подстановка имеет более сложный вид. Например, в системе:
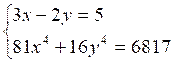
замена 3x=u, -2y=v, позволяет симметричную систему
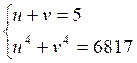
Иногда, введением вспомогательных неизвестных можно свести уравнение с одним неизвестным к симметричной системе двух уравнений с двумя неизвестными.
Лекция 4: Решение систем уравнений от трех переменных
Теорема 2. Пусть ![]()
![]() ,
,![]() ,
,![]() - три произвольных числа. Кубическое уравнение
- три произвольных числа. Кубическое уравнение
![]() =0
=0![]()
и система уравнений 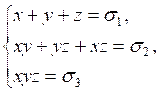
![]()
связаны друг с другом следующим образом: если ![]() корни кубического уравнения, то система уравнений
корни кубического уравнения, то система уравнений ![]() имеет шесть решений
имеет шесть решений
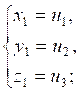
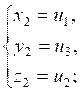
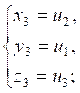
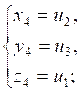
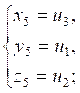
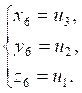
(получающихся друг из друга перестановками) и других решений не имеет; обратно, если ![]() ,
, ![]() -решение системы
-решение системы ![]() , то числа
, то числа ![]() являются корнями кубического уравнения
являются корнями кубического уравнения ![]() .
.
Лемма. Если ![]() корни кубического уравнения
корни кубического уравнения ![]() , то имеют место следующие соотношения:
, то имеют место следующие соотношения: ![]() ,
, ![]() ,
, ![]() .
.
Эти соотношения называют формулами Виета для кубического уравнения. Покажем, откуда эти соотношения вытекают. Итак, пусть ![]() корни кубического уравнения
корни кубического уравнения ![]() , тогда
, тогда
![]() .
.
Раскрывая скобки в правой части, находим:
![]() .
.
Из равенства многочленов следует равенства соответствующих коэффициентов, т.е.
![]() ,
,
![]() ,
,
![]() ,
,
что и доказывает лемму.
Лекция 5: Возвратные уравнения. Теорема Виета.
Симметрические многочлены можно применять и для решения некоторых видов уравнений высших степеней.
Рассмотрим так называемые возвратные уравнения.
Назовем многочлен ![]()
![]() (
(![]() ) возвратным, если в нем коэффициенты, равноудаленные от концов, совпадают, т.е.
) возвратным, если в нем коэффициенты, равноудаленные от концов, совпадают, т.е. ![]() ,
, ![]() ,
, ![]() , …
, …
Например, возвратным является многочлены:
![]() ,
,
![]() ,
,
![]()
Уравнение ![]() , левая часть которого представляет собой возвратный многочлен, называется возвратным.
, левая часть которого представляет собой возвратный многочлен, называется возвратным.
В основе решения возвратных уравнений лежит следующая
Теорема 3. Всякий возвратный многочлен ![]() четной степени 2k представляется в виде f(z)=
четной степени 2k представляется в виде f(z)=![]() , где
, где 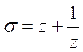 и
и ![]() - некоторый многочлен степени k от
- некоторый многочлен степени k от![]() .
.
Всякий возвратный многочлен f(z) нечетной степени делится на z+1, причем частное представляет собой возвратный многочлен четной степени.
Доказательство теоремы рассмотрено в Приложение 12.
Полагая 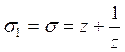 ,
, ![]() , получаем
, получаем
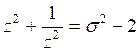
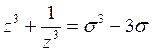
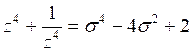 и так далее.
и так далее.
Целая серия задач, в которых требуется вычислить некоторые выражения, содержащие корни заданного квадратного уравнения, содержащие корни заданного уравнения, также с успехом решается при помощи симметрических многочленов. Рассмотрим два примера.
Пример 1. Дано квадратное уравнение ![]() ; составить новое квадратное уравнение, корнями которого является квадраты корней данного уравнения.
; составить новое квадратное уравнение, корнями которого является квадраты корней данного уравнения.
Решение.
Для решения этой задачи обозначим корни данного уравнения через ![]() , корни исходного – через
, корни исходного – через ![]() . По теореме Виета
. По теореме Виета
![]()
![]()
и точно так же,
![]() ,
, ![]()
Но, по условию задачи, имеем ![]() и потому
и потому
![]()
![]() .
.
Таким образом, искомое квадратное уравнение имеет вид
![]()
Тем же методом можно решить и более сложные задачи. Рассмотрим следующий пример.
Пример 2.
Составить квадратное уравнение ![]() корнями которого являются числа
корнями которого являются числа ![]() где
где ![]() - корни квадратного уравнения
- корни квадратного уравнения ![]()
Решение. Для решения снова воспользуемся формулами Виета, согласно которым
![]()
С другой стороны, по тем же формулам,
![]()
![]()
Воспользуемся таблицей Приложения 1, легко выразим симметрические многочлены ![]() через
через ![]() и, подставив значения
и, подставив значения ![]() , вычислим интересующие нас коэффициенты
, вычислим интересующие нас коэффициенты![]() . Имеем
. Имеем
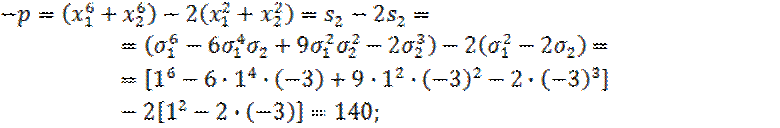
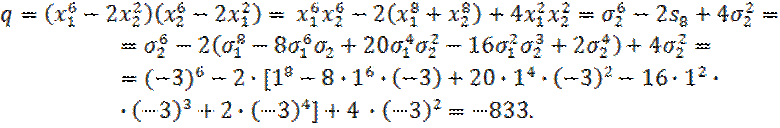
Таким образом, ![]() , и потому искомое квадратное уравнение имеет вид
, и потому искомое квадратное уравнение имеет вид ![]()
Лекция 6: Доказательство неравенств
Симметрические многочлены применяются и для доказательства неравенств, используя выражение степенных сумм через ![]() и следующую теорему.
и следующую теорему.
Теорема 4. Пусть ![]() - действительные числа. Для того чтобы оба числа x, y, определяемые из системы уравнений
- действительные числа. Для того чтобы оба числа x, y, определяемые из системы уравнений 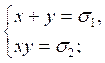 были действительными, необходимо и достаточно, чтобы
были действительными, необходимо и достаточно, чтобы![]() удовлетворяли неравенству
удовлетворяли неравенству ![]() .
.
Равенство ![]() достигается лишь в случае, если x=y. Для того чтобы оба числа x,y, были действительными и неотрицательными, необходимо и достаточно, чтобы числа
достигается лишь в случае, если x=y. Для того чтобы оба числа x,y, были действительными и неотрицательными, необходимо и достаточно, чтобы числа ![]() удовлетворяли неравенствам
удовлетворяли неравенствам ![]() ,
, ![]() ,
, ![]()
Доказательство. Числа a и b, являются, в силу теоремы 1, корнями квадратного уравнения
![]() ,
,
т.е. совпадают с числами
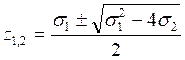 .
.
Поэтому для того, чтобы корни квадратного уравнения x,y были действительные числа необходимо и достаточно, чтобы подкоренное выражение было не отрицательным, т.е. чтобы выполнялось неравенство ![]() . Равенство
. Равенство ![]() означает, что оба корня квадратного уравнения совпадают, т.е. x=y.
означает, что оба корня квадратного уравнения совпадают, т.е. x=y.
Если числа x,y не отрицательные, то, неравенство ![]() выполняется еще неравенства
выполняется еще неравенства ![]() ,
,![]() Пусть теперь, обратное, выполняются неравенства
Пусть теперь, обратное, выполняются неравенства ![]() ,
,![]() ,
,![]() Как было показано выше, из первого неравенства следует, что числа x
и
y действительные; так как
Как было показано выше, из первого неравенства следует, что числа x
и
y действительные; так как ![]() , то оба они имеют одинаковый знак; наконец, из соотношения
, то оба они имеют одинаковый знак; наконец, из соотношения ![]() вытекает, что они неотрицательные. Теорема доказана.
вытекает, что они неотрицательные. Теорема доказана.
Пример. Доказать, что при любых действительных ![]() a
и b
справедливо неравенство
a
и b
справедливо неравенство ![]() .
.
Решение: Рассмотрим разность
![]()
![]()
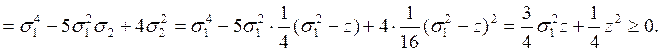
Следовательно неравенство ![]() верно.
верно.
Поможем написать любую работу на аналогичную тему

