Семинары №1,2,3
Выразить через ![]() степенные суммы s1, s2, s3, s4, s5 от x,y.
степенные суммы s1, s2, s3, s4, s5 от x,y.
Выразить через ![]()
![]() степенные суммы s4, s5, s6, s7, s8 от x,y,z.
степенные суммы s4, s5, s6, s7, s8 от x,y,z.
Семинары №4,5 Разложение симметрических многочленов на множители
Прием заключается в том, что рассматриваемый симметрический многочлен выражают через ![]() и затем полученное выражение разлагают на множители. При выражение симметрического многочлена четвертой степени через
и затем полученное выражение разлагают на множители. При выражение симметрического многочлена четвертой степени через ![]() получается многочлен второй степени относительно
получается многочлен второй степени относительно ![]() . Для разложение его на множители достаточно найти корни полученного многочлена второй степени.
. Для разложение его на множители достаточно найти корни полученного многочлена второй степени.
Задание 1. Разложить на множители многочлен
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
Замечание: Решение задания1 (a-d) рассмотрено в Приложение 5
Семинары №6,7 Освобождение от иррациональности в знаменателе выражения
Симметрические многочлены позволяют решать многие трудные задачи на освобождение от иррациональности в знаменателе.
В случае, когда знаменатель имеет вид ![]() или
или ![]() Эту задачу можно решить и без применения симметрических многочленов. Для этого достаточно использовать формулы:
Эту задачу можно решить и без применения симметрических многочленов. Для этого достаточно использовать формулы:
![]()
![]() (
(![]() );
);
![]()
Например, если надо освободиться от иррациональности в знаменателе выражения
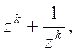 ,
,
то сначала умножаем числитель и знаменатель на «сопряженное выражение » ![]() (что приводит знаменатель к виду
(что приводит знаменатель к виду ![]() ), а потом - на
), а потом - на ![]() . Мы получаем:
. Мы получаем:
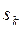
Теперь уже можно использовать вторую из приведенных выше формул. Положим в ней ![]() . Тогда ясно, что надо умножить числитель и знаменатель на выражение
. Тогда ясно, что надо умножить числитель и знаменатель на выражение
![]() +
+![]()
После умножения получим:
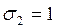
Сложнее обстоит дело, если знаменатель состоит из трех или большего числа иррациональных слагаемых. Здесь-то могут помочь симметрические многочлены.
Задание 2. Освободиться от иррациональности в знаменателе выражения.
a) ![]()
b) 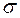
Замечание: Решение задания 2 рассмотрено в Приложение 6
Семинары №8,9 Решение систем уравнений от двух переменных
Задание 3. Решить систему уравнений
a) 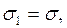
b) 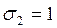
c) 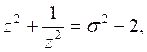
d) 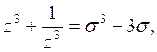
e) 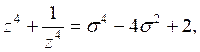
Замечание: Решение задания 3 рассмотрено в Приложение 7
Семинар №10 Решение систем уравнений от трех переменных
Задание 4. Решить систему уравнений.
a) 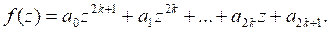
b) 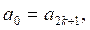
c) 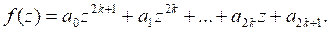
Замечание: Решение задания 4 рассмотрено в Приложение 8
Семинары №11,12,13 Решение возвратных уравнений
Задание 5. Решить уравнение
a) ![]()
b) ![]() +9=0
+9=0
c) ![]()
Замечание: Решение задания 5 рассмотрено в Приложение 9
Семинары №14,15 Доказательство неравенств
Задание 6. Доказать, что если a,b
- действительные числа, удовлетворяющие условию ![]() , то справедливы неравенства:
, то справедливы неравенства:
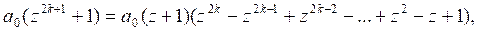 ,
, 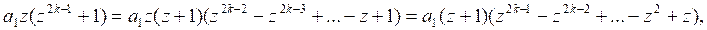 ,
, 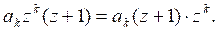
Задание 7. Доказать, что при любых неотрицательных a и b справедливо неравенство:
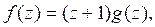
Задание 8. Доказать, что при любых неотрицательных a и b справедливо неравенство:
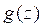
Задание 9. Доказать, что для любых действительных чисел a, b, c справедливо неравенство:
![]()
Замечание: Решение задания 6,7,8,9 рассмотрено в Приложение 10
Семинар №16,17 Доказательство тождеств
Задание 10. Доказать, что если 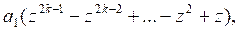 то для любого нечетного n справедливо тождество
то для любого нечетного n справедливо тождество
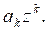
Задание 11. Доказать, что если ![]() , то
, то
![]() .
.
Задание 12. Доказать, что если
![]() ,
,
то ![]() .
.
Задание 13. Докажите тождество
![]() .
.
Замечание: Решение задания 10, 11, 12, рассмотрено в Приложение 11.
Примерные варианты индивидуальных домашних заданий.
Вариант №1
1. Разложите симметрический многочлен на множители.
![]()
2. Освободитесь от иррациональности в знаменателе выражения.
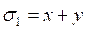 .
.
3. Решите системы уравнений.
1.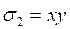 2.
2. 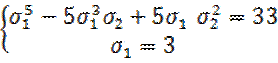 .
.
4. Решите уравнения.
![]() .
.
5. Докажите тождество
![]()
Вариант №2
1.Разложите симметрический многочлен на множители
![]() .
.
2.Освободитесь от иррациональности в знаменателе выражения
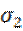 .
.
3. Решите системы уравнений
1. 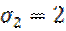 2.
2. 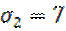
4. Решите уравнения
![]() .
.
5. Докажите неравенство
![]()
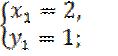 .
.
Поможем написать любую работу на аналогичную тему

