Значимость коэффициентов простой линейной регрессии (ŷ = b0+b1 ·х) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия:
для параметра b0
(1)
для параметра b1
(2)
Соответствующие средние квадратические отклонения определяются по следующим формулам:
(3)
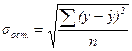(4)
σост., σх – средние квадратические отклонения.
Вычисленные по формулам и значения, сравнивают с критическими t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости, а и числом степеней свободы вариации.
|
Число степеней свободы |
Вероятность |
|||||||||||
|
0,1 |
0,2 |
0,3 Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
1 |
0,16 |
0,32 |
0,51 |
0,73 |
1,00 |
1,38 |
1,96 |
3,08 |
6,31 |
12,71 |
31,82 |
63,66 |
|
2 |
0,14 |
0,29 |
0,44 |
0,62 |
0,82 |
1,06 |
1,31 |
1,89 |
2,92 |
4,30 |
6,96 |
9,92 |
|
3 |
0,14 |
0,28 |
0,42 |
0,58 |
0,76 |
0,98 |
1,25 |
1,64 |
2,35 |
3,18 |
4,54 |
5,84 |
|
4 |
0,13 |
0,27 |
0,41 |
0,57 |
0,74 |
0,94 |
1,19 |
1,53 |
2,13 |
2,78 |
3,75 |
4,60 |
|
5 |
0,13 |
0,27 |
0,41 |
0,56 |
0,73 |
0,92 |
1,16 |
1,48 |
2,01 |
2,57 |
3,36 |
4,03 |
|
6 |
0,13 |
0,26 |
0,40 |
0,55 |
0,72 |
0,91 |
1,13 |
1,44 |
1,94 |
2,45 |
3,14 |
3,71 |
|
7 |
0,13 |
0,26 |
0,40 |
0,55 |
0,71 |
0,90 |
1,12 |
1,41 |
1,89 |
2,36 |
3,00 |
3,50 |
|
8 |
0,13 |
0,26 |
0,40 |
0,55 |
0,70 |
0,89 |
1,11 |
1,40 |
1,86 |
2,31 |
2,90 |
3,35 |
|
9 |
0,13 |
0,26 |
0,40 |
0,54 |
0,70 |
0,88 |
1,10 |
1,38 |
1,83 |
2,26 |
2,82 |
3,25 |
|
10 |
0,13 |
0,26 |
0,40 |
0,54 |
0,70 |
0,88 |
1,09 |
1,37 |
1,81 |
2,23 |
2,76 |
3,17 |
|
11 |
0,13 |
0,26 |
0,40 |
0,54 |
0,70 |
0,88 |
1,09 |
1,36 |
1,80 |
2,20 |
2,72 |
3,11 |
|
12 |
0,13 |
0,26 |
0,39 |
0,54 |
0,69 |
0,87 |
1,08 |
1,36 |
1,78 |
2,18 |
2,68 |
3,05 |
|
13 |
0,13 |
0,26 |
0,39 |
0,54 |
0,69 |
0,87 |
1,08 |
1,35 |
1,77 |
2,16 |
2,65 |
3,01 |
|
14 |
0,13 |
0,26 |
0,39 |
0,54 |
0,69 |
0,87 |
1,08 |
1,34 |
1,76 |
2,14 |
2,62 |
2,98 |
|
15 |
0,13 |
0,26 |
0,39 |
0,54 |
0,69 |
0,87 |
1,07 |
1,34 |
1,75 |
2,13 |
2,60 |
2,95 |
|
16 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,07 |
1,34 |
1,75 |
2,12 |
2,58 |
2,92 |
|
17 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,07 |
1,33 |
1,74 |
2,11 |
2,57 |
2,90 |
|
18 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,07 |
1,33 |
1,73 |
2,10 |
2,55 |
2,88 |
|
19 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,07 |
1,33 |
1,73 |
2,09 |
2,54 |
2,86 |
|
20 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,06 |
1,32 |
1,72 |
2,09 |
2,53 |
2,84 |
|
21 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,06 |
1,32 |
1,72 |
2,08 |
2,52 |
2,83 |
|
22 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,06 |
1,32 |
1,72 |
2,07 |
2,51 |
2,82 |
|
23 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,86 |
1,06 |
1,32 |
1,71 |
2,07 |
2,50 |
2,81 |
|
24 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,86 |
1,06 |
1,32 |
1,71 |
2,06 |
2,49 |
2,80 |
|
25 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,86 |
1,06 |
1,32 |
1,71 |
2,06 |
2,48 |
2,79 |
|
26 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,86 |
1,06 |
1,31 |
1,71 |
2,06 |
2,48 |
2,78 |
|
27 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,85 |
1,06 |
1,31 |
1,70 |
2,05 |
2,47 |
2,77 |
|
28 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,85 |
1,06 |
1,31 |
1,70 |
2,05 |
2,47 |
2,76 |
|
29 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,85 |
1,05 |
1,31 |
1,70 |
2,04 |
2,46 |
2,76 |
|
30 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,85 |
1,05 |
1,31 |
1,70 |
2,04 |
2,46 |
2,75 |
|
40 |
0,13 |
0,25 |
0,39 |
0,53 |
0,68 |
0,85 |
1,05 |
1,30 |
1,68 |
2,02 |
2,42 |
2,70 |
|
60 |
0,13 |
0,25 |
0,39 |
0,53 |
0,68 |
0,85 |
1,05 |
1,30 |
1,67 |
2,00 |
2,39 |
2,66 |
|
120 |
0,13 |
0,25 |
0,39 |
0,53 |
0,68 |
0,84 |
1,04 |
1,29 |
1,66 |
1,98 |
2,36 |
2,62 |
|
8 |
0,13 |
0,25 |
0,38 |
0,52 |
0,67 |
0,84 |
1,04 |
1,28 |
1,64 |
1,96 |
2,33 |
2,58 |
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.
Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении.
При линейной однофакторной связи t-критерий можно рассчитать по формуле:
(5)
где (n-2) - число степеней свободы при заданном уровне значимости а и объеме выборки п.
Полученное значение tрасч. сравнивают с табличным значением t-критерия (для а = 0,05 и 0,01). Если рассчитанное значение tрасч. превосходит табличное значение критерия tтабл., то практически невероятно, что найденное значение обусловлено только случайными колебаниями (то есть отклоняется гипотеза о его случайности).
После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего, нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель).
Для удобства интерпретации параметра b1 используют коэффициент эластичности, который показывает средние среднее изменение результативного признака ŷ при изменении факторного признака x1 на 1%.
В общем виде коэффициент эластичности имеет следующий вид:
(6)
где b1 – коэффициент уравнения парной регрессии; 
– среднее значение независимого фактора;
– среднее значение изучаемого показателя.
Поможем написать любую работу на аналогичную тему