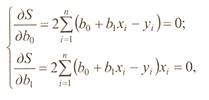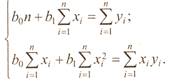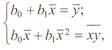Параметры уравнения ŷ = b0 +b1 · х (b0, b1) находят методом наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений).
Метод наименьших квадратов.
Итак,
|
|
(1) |
На основании необходимого экстремума функции двух переменных S=S(b0, b1) приравниваем к 0 её частные производные:
|
|
(2) |
откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:
|
|
(3) |
Теперь разделив обе части уравнения на n, получим систему нормальных уравнений в виде:
|
|
(4) |
Таким образом, имеем:
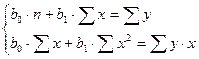 (5)
(5)
При линейной форме корреляции применяют различные коэффициенты тесноты связи.
Наиболее распространённым является линейный коэффициент корреляции, предложенный английским математиком К. Пирсоном. Данный коэффициент принимает значения в интервале ![]() .
.
Он определяется следующим образом:
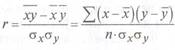
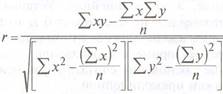
Отрицательные значения указывают на обратную связь, положительные –на прямую.
При r=0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. И, наконец, при r = ±1 связь является функциональной.
Поможем написать любую работу на аналогичную тему