Аналитическое выравнивание и кривые роста.

При наличии тенденции в ряду динамики его уровни можно рассматривать как функцию времени (t) и случайной компоненты (ε).

В настоящее время компьютерные программы анализа временных рядов предлагают достаточно широкий набор математических функций для построения уравнения тренда. Наиболее часто используются полиномы K-й степени, экспоненты, различного рода кривые с насыщением.

В общем виде полином K-й степени представляет собой выражение:

                                               у = а0 +alt + a2t2+...+aktk                           (1)

 При К= 1 получаем линейный тренд:

                                                ŷ = а0 +a1t                                       (2)

По содержанию линейный тренд означает, что уровни динамического ряда изменяются с одинаковой скоростью. В этом можно убедиться, если в уравнение линейного тренда ŷ = а0 +a1∙t подставить порядковые значения t.

Параметр а0 означает начальный уровень тренда при t = 0. Параметр а1 характеризует средний абсолютный прирост в единицу времени t.

В линейном тренде уровни динамического ряда изменяются в арифметической прогрессии. Это означает, что при прогнозировании по линейному тренду предполагаются падающие темпы роста уровня временного ряда.

При К=2 получаем параболу второй степени: ŷt =a0 +alt + a2t2. Данная функция рекомендуется для прогнозирования, если ряд характеризуется стабильным абсолютным ускорением, то есть постоянными являются вторые разности (приросты абсолютных приростов).

Убедимся в этом, подставив в уравнение параболы второй степени порядковые значения t:

Разобрать самостоятельно и вывести Δ для

1. ŷt =a0 +al∙t + a2∙t2+ a3∙t3 (Δ`` = 6a3)

2. ŷt =a·bt (коэффициент роста = b)

Применяя метод наименьших квадратов к линейной, параболической, кубической, показательной, логарифмической, гиперболической и другим функциям, имеем

     а) Уравнение линейного тренда имеет следующий вид:

                                           у = а + b ∙ x                                                (3)

         Система линейных уравнений для нахождения параметров a и b следующая:

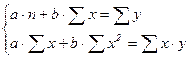                                                                           (4)

где n – количество месяцев.

     б) Уравнение параболического тренда имеет следующий вид:

                                           у = а + b ∙ x + с ∙ х2                                      (5)

         Система линейных уравнений для нахождения параметров a, b и с следующая:

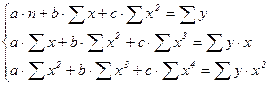                                                           (6)

где n – количество месяцев.

     в) Уравнение тренда кубической параболы имеет следующий вид:

                                 у = а + b ∙ x + с ∙ х2 + d ∙ х3                                    (7)

         Система линейных уравнений для нахождения параметров a, b, с и d следующая:

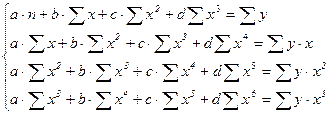                                               (8)

где n – количество месяцев.

     г) Уравнение тренда показательной функции имеет следующий вид:

                                                    у = а · bx                                                      (9)

         Система линейных уравнений для нахождения параметров a и b следующая:

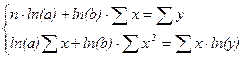                           (10)

где n – количество месяцев.

     д) уравнение тренда логарифмической параболы имеет следующий вид:

                                                                                      (11)

Система линейных уравнений для нахождения параметров a и b следующая:

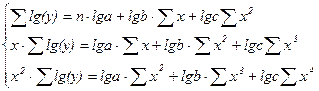            (12)

где n – количество месяцев.

         е) Система линейных уравнений для нахождения параметров a и b уравнения тренда функции

                                           у = а + b · ln(x)                                           (13)

имеет следующий вид:

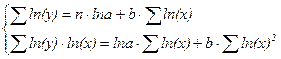                   (14)

где n – количество месяцев.

         ж) Уравнение равносторонней гиперболы имеет следующий вид:

                                           у = а + b/x                                                  (15)

         Система линейных уравнений для нахождения параметров a и b следующая:

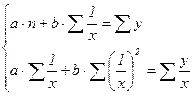                                                                          (16)

где n – количество месяцев.

     з) Уравнение неравносторонней гиперболы имеет следующий вид:

                                                                                            (17)

         Система линейных уравнений для нахождения параметров a и b следующая:

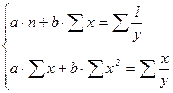                                                                              (18)

где n – количество месяцев.

     и) Уравнение неравносторонней гиперболы имеет следующий вид:

                                                                                            (19)

         Система линейных уравнений для нахождения параметров a и b следующая:

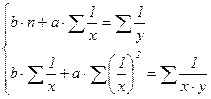                                                                       (20)

где n – количество месяцев.

     к) ряд Фурье (в случае одной гармоники) имеет следующий вид:

                                 уx = a0 + a1 · cos(x) + b1 · sin(x)                    (21)

         Система линейных уравнений для нахождения параметров a, b и с следующая:

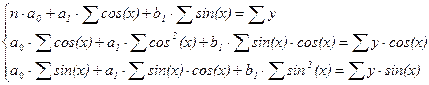         (22)