На основе уравнения тренда дается точечная оценка прогноза. Однако более надежный прогноз предполагает оценку его в интервале, ибо полное совпадение фактического и прогнозируемого уровней динамического ряда (уt и уp) маловероятно. Даже если выбор формы уравнения тренда удачен, фактическая реализация события может отличаться от прогнозируемой, ибо тренд характеризует лишь тенденцию, а уровни временного ряда содержат также случайную компоненту (ε), то есть yt =f(t,ε). Наличие ее, а также возможная ошибка параметров тренда, оцениваемых по ограниченному числу наблюдений, учитываются в доверительном интервале прогноза.
В основе расчета доверительного интервала прогноза лежит показатель колеблемости уровней динамического ряда относительно тренда (Sy). Чем больше этот показатель, тем шире интервал прогноза при одной и той же степени вероятности. Колеблемость уровней динамического ряда относительно тренда определяется формулой:
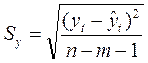 (1)
(1)
где yt, - фактические уровни динамического ряда; ŷt – расчетные значения уровней динамического ряда по уравнению тренда; n – длина динамического ряда; т – число параметров в уравнении тренда (без свободного члена).
Доверительный интервал для тренда определяется следующим неравенством:
ŷt ± ta · Sy (2)
где ta- табличное значение критерия Стьюдента.
Поможем написать любую работу на аналогичную тему

