Как будут выглядеть результаты множественной регрессии?

Прежде всего, мы приведем краткий обзор входных данных и основных результатов. Более подробное их объяснение будет дано позже.

Пусть k означает количество поясняющих переменных (Х- переменных); k может быть любым разумным числом. Ваши элементарные единицы нередко называются наблюдениями; это могут быть клиенты, фирмы, выпускаемые изделия и т.п. По "техническим" причинам у вас должно быть, по крайней мере, на одно наблюдение больше, чем имеется Х- переменных, т.е. n > k+1. Практические соображения диктуют необходимость намного большего числа наблюдений.

Входные данные для обычного множественного регрессионного анализа представлены в табл. 1.

Таблица 1. Входные данные для множественной регрессии

Сдвиг, или постоянный член, a, определяет прогнозируемое значение Y, когда все переменные X равны 0. Коэффициент регрессии для каждой X-переменной определяет влияние этой Х- переменной на Y при условии, что все остальные Х- переменные не меняются: коэффициент регрессии bj для j-ой X- переменной указывает, какое увеличение Y ожидается, когда все Х- переменные остаются неизменными, за исключением переменной Хj, которая увеличивается на одну единицу. Взятые вместе эти коэффициенты регрессии составляют уравнение прогнозирования, или уравнение регрессии, вида

прогнозируемое значение Y = а + b1X1 + b2X2 + ... + bkXk ,

которое можно использовать в целях прогнозирования или управления. Эти коэффициенты (а, b1, b2, ... bk) обычно вычисляются методом наименьших квадратов, который минимизирует сумму квадратов ошибок прогнозирования. Как известно, в основе процедуры МНК лежит решение системы нормальных уравнений. Например, для трех факторной регрессии система нормальных уравнений будет выглядеть следующим образом:

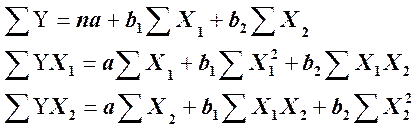
Решение данной системы не представляет большой сложности, но при наличии персонального компьютера нахождение коэффициентов а, b1, b2, ... bk не предусматривает наличия даже элементарных навыков в области МНК, – все процессы выполняются в автоматическом режиме.

Как и в случае простой регрессии (с единственной Х- переменной), стандартная ошибка оценки, Se указывает приблизительную величину ошибок прогнозирования. И как в случае простой регрессии, R2 является коэффициентом детерминации, который указывает, какой процент вариации Y «объясняется» всеми Х- переменными. В данном случае речь идет не просто о квадрате коэффициента корреляции Y с одной Х- переменной, а о квадрате коэффициента корреляции r переменной Y (фактических значений) с прогнозами (которые вычисляются с помощью уравнения регрессии, найденного методом наименьших квадратов). Такой показатель учитывает все Х- переменные.

Статистический вывод начинается с общей проверки, которую называют F-тестом (F-test). Цель F-теста заключается в том, чтобы выяснить, объясняют ли Х- переменные значимую долю вариации Y. Если ваша регрессия не является значимой, говорить больше не о чем. Если же регрессия оказывается значимой, можно продолжить анализ статистических выводов, используя t-тесты для отдельных коэффициентов регрессии, которые показывают, насколько значимой является влияние той или иной Х- переменной на Y при условии, что все другие Х- переменные остаются неизменными. Построение доверительных интервалов и проверки гипотез для отдельного коэффициента регрессии будут, конечно же, основываться на его стандартной ошибке. Каждый коэффициент регрессии имеет свою стандартную ошибку; они обозначаются Sb1, Sb2, ... , Sbk.