Тремя основными целями анализа двумерных данных, представленных парами (Х, У), являются: (1) описание и понимание взаимосвязи, (2) прогнозирование и предсказание нового наблюдения и (3) корректировка и управление процессом.
Корреляционный анализ позволяет сделать вывод о силе взаимосвязи, а регрессионный анализ используется для прогнозирования одной переменной на основании другой (как правило, У на основании X).
Двумерные данные анализируют с использованием диаграммы рассеяния в координатах У и X, которая дает визуальное представление о взаимосвязи в данных. Корреляция, или точнее линейный коэффициент корреляции (г), представляет собой безразмерное (не имеющее единиц измерения) число в диапазоне от -1 до 1, которое характеризует силу взаимосвязи. Равенство коэффициента корреляции 1 свидетельствует об идеальной взаимосвязи в виде прямой линии с наклоном вверх. Равенство коэффициента корреляции -1 свидетельствует об идеальной взаимосвязи в виде наклоненной вниз (отрицательно) прямой линии. Коэффициент корреляции говорит о том, насколько близко к этой наклоненной прямой линии расположены точки диаграммы, однако он не характеризует крутизну наклона этой линии. Формула вычисления коэффициента корреляции для тех, кто умеет пользоваться Excel имеет следующий вид:
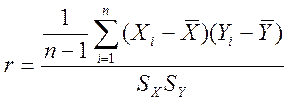 .
.
Ковариация X и У представляет собой числитель в формуле для коэффициента корреляции. Поскольку единицы измерения ковариации трудно интерпретировать, удобнее работать с коэффициентом корреляции.
Корреляцию нельзя рассматривать как причинную обусловленность. Коэффициент корреляции характеризует связь между числами, но не объясняет ее. Корреляция может быть вызвана тем, что переменная X влияет на У, или тем, что переменная У влияет на X. Кроме того, корреляция может быть вызвана также тем, что на X и У влияет некий скрытый "третий фактор", что создает впечатление связи между X и У. Термином ложная корреляция обозначают высокую корреляцию, которая возникает благодаря действию некоторого третьего фактора.
Поможем написать любую работу на аналогичную тему

