Регрессионный анализ заключается в прогнозировании одной переменной на основании другой. Линейный регрессионный анализ прогнозирует значение одной переменной на основании другой с помощью прямой линии. Наклон этой линии, выражается в единицах измерения У на одну единицу X и характеризует крутизну подъема или спуска (если b отрицательное) линии. Сдвиг, a, равен значению, которое принимает У при X, равном 0. Уравнение прямой линии имеет следующий вид:
Y = Сдвиг + (Наклон)(Х) = а + bХ .
Линия наименьших квадратов характеризуется наименьшей из всех возможных линий суммой возведенных в квадрат ошибок прогнозирования по вертикали и используется как лучшая линия прогнозирования, основанная на данных. Наклон этой линии, b, называют также коэффициентом регрессии У по X, а сдвиг а (отрезок отсекаемый на оси У) называют также постоянным членом регрессии. Ниже приведены уравнения для наклона и сдвига, соответствующие линии наименьших квадратов.
Наклон равен: 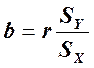 .
.
Сдвиг равен: 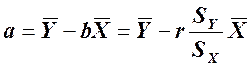 .
.
Формула для линии наименьших квадратов имеет следующий вид:
Прогнозируемое значение У равно:
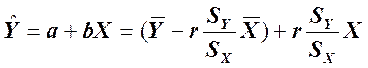 .
.
Прогнозируемое значение для У при заданном значении X определяется путем подстановки этого значения X в уравнение для линии наименьших квадратов. Каждая из точек данных характеризуется остатком – ошибкой прогнозирования, указывающей, насколько выше или ниже линии находится точка.
Поможем написать любую работу на аналогичную тему

