Существуют две меры соответствия линии наименьших квадратов имеющимся данным. Стандартная ошибка оценки (или предсказания), которую обозначают 
, приблизительно указывает величину ошибок прогнозирования (остатков) для имеющихся данных в тех же единицах, в которых измерена и переменная У. Соответствующие формулы приведены ниже.
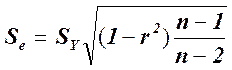(для вычисления)
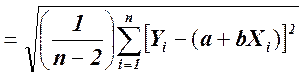(для интерпретации).
Значение 
, часто называемое коэффициентом детерминации, говорит о том, какой процент вариации У объясняется поведением X.
Доверительные интервалы и проверка гипотез для коэффициента регрессии связаны с определенными предположениями относительно анализируемой совокупности данных, которые должны гарантировать, что она состоит из независимых наблюдений, характеризующихся линейной взаимосвязью с равной вариацией и приблизительно нормально распределенной случайностью. Во-первых, эти данные должны представлять собой произвольную выборку из интересующей нас генеральной совокупности. Во-вторых, линейная модель указывает, что наблюдаемое значение У определяется взаимосвязью в генеральной совокупности плюс случайная ошибка, имеющая нормальное распределение. Существуют параметры генеральной совокупности, соответствующие наклону и сдвигу линии наименьших квадратов, построенной на данных выборки:
Y = (α+βХ)+ε =
= (Взаимосвязь в генеральной совокупности) + случайность.
где ε имеет нормальное распределение со средним значением, равным 0, и постоянным стандартным отклонением σ.
Статистические выводы (использование доверительных интервалов и проверки статистических гипотез) относительно коэффициентов линии наименьших квадратов основываются, как обычно, на их стандартных ошибках и значениях из t-таблицы для п - 2 степеней свободы. Стандартная ошибка коэффициента наклона, 
, указывает приблизительную величину отклонения оценки наклона, b (коэффициент регрессии, вычисленный на основе данных выборки), от наклона в генеральной совокупности, β, вызванного случайным характером выборки. Стандартная ошибка сдвига, 
, указывает приблизительно, насколько далеко оценка сдвига а отстоит от истинного сдвига α в генеральной совокупности. Соответствующие формулы выглядят следующим образом:
стандартная ошибка коэффициента регрессии b:
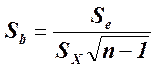
стандартная ошибка сдвига:
.
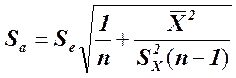Доверительный интервал для наклона в генеральной совокупности, β:
от 
до 
.
Доверительный интервал для сдвига в генеральной совокупности, α:
от 
до 
.
Один из способов проверки, является ли обнаруженная взаимосвязь между X и У реальной или это просто случайное совпадение, заключается в сравнении β с заданным значением β0 = 0. О значимой связи можно говорить в том случае, если 0 не попадает в доверительный интервал, базирующийся на b и Sb, или если абсолютное значение t = b/Sb превосходит соответствующее t-значение в t-таблице.
t – таблица (t - критерий Стьюдента)
|
Доверительный интервал |
|||||||
|
Двухсторонний |
80% |
90% |
95% |
98% |
99% |
99,8% |
99,9% |
|
Односторонний |
90% |
95% |
97,5% |
99% |
99,5% |
99,9% |
99,95% |
|
Уровень значимости проверки гипотезы |
|||||||
|
Двухсторонний тест |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,002 |
0,001 |
|
Односторонний тест |
0,10 |
0,05 |
0,025 |
0,01 |
0,005 |
0,001 |
0,0005 |
|
В целом: степени свободы |
Критические значения t |
||||||
|
1 |
3,078 |
6,314 |
12,706 |
31,821 |
63,657 |
318,309 |
636,619 |
|
2 |
1,886 |
2,920 |
4,303 |
6,965 |
9,925 |
22,327 |
31,599 |
|
3 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
10,215 |
12,924 |
|
4 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
7,173 |
8,610 |
|
5 |
1,476 |
2,015 |
2,571 |
3,365 |
4,032 |
5,893 |
6,869 |
|
6 |
1,440 |
1,943 |
2,447 |
3,143 |
3,707 |
5,208 |
5,959 |
|
7 |
1,415 |
1,895 |
2,365 |
2,998 |
3,499 |
4,785 |
5,408 |
|
8 |
1,397 |
1,860 |
2,306 |
2,896 |
3,355 |
4,505 |
5,041 |
|
9 |
1,383 |
1,833 |
2,262 |
2,821 |
3,250 |
4,297 |
4,781 |
|
10 |
1,372 |
1,812 |
2,228 |
2,764 |
3,169 |
4,144 |
4,587 |
|
11 |
1,363 |
1,796 |
2,201 |
2,718 |
3,106 |
4,025 |
4,437 |
|
12 |
1,356 |
1,782 |
2,179 |
2,681 |
3,055 |
3,930 |
4,318 |
|
13 |
1,350 |
1,771 |
2,160 |
2,650 |
3,012 |
3,852 |
4,221 |
|
14 |
1,345 |
1,761 |
2,145 |
2,624 |
2,977 |
3,787 |
4,140 |
|
15 |
1,341 |
1,753 |
2,131 |
2,602 |
2,947 |
3,733 |
4,073 |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
38 |
1,304 |
1,686 |
2,024 |
2,429 |
2,712 |
3,319 |
3,566 |
|
39 |
1,304 |
1,685 |
1,023 |
2,426 |
2,708 |
3,313 |
3,558 |
|
Бесконечность |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
3,090 |
3,291 |
Эта проверка эквивалентна проверке значимости коэффициента корреляции и означает, по сути, то же самое, что и F-тест для случая, когда уравнение содержит только одну переменную X. Разумеется, любой из коэффициентов (a или b) можно сравнить с любым подходящим заданным значением, воспользовавшись одно- или двусторонней проверкой (в зависимости от конкретных обстоятельств) и с использованием тех же методов проверки, что были рассмотрены для среднего генеральной совокупности.
Поможем написать любую работу на аналогичную тему