В ДА основной интерес представляет не столько сами оценки, сколько их сравнение и, в первую очередь, проверка гипотезы Н0: а1=а2=…=ар=0, означающей одинаковость, неразличимость, воздействий всех р уровней. Со статистической точки зрения задачу ДА можно сформулировать так: для каждой из р генеральных совокупностей получено по выборке объемом Ni и необходимо сопоставить р значений выборочных средних.
ДА базируется на разложении общей суммы квадратов S0
отклонений наблюдений 
от общего среднего 
на составляющие, связанные с рассеянием между уровнями Sму
и рассеянием внутри отдельных уровней Sву:
, Sму=
, Sву=
.
Подобное разложение получается следующим образом. Обе части тождества 
возводят в квадрат и суммируют по i и j:
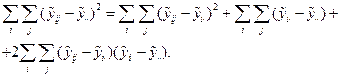(5.4)
Последнее слагаемое в правой части формулы (5.4) обращается в нуль в силу выполнения следующей очевидной цепочки равенств:
.
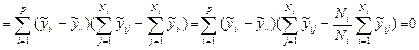Соотношение (5.4) приобретает вид S0=Sму+Sву. Суммы S0 ,Sму ,Sву имеют N-1, p-1, N-p степеней свободы соответственно. Если имеет место проверяемая гипотеза Н0, то каждое из отношений:
может служить оценкой дисперсии s2 случайных возмущений. В силу нормальности возмущений отношение 
имеет F-распределение. Полученные значения представляют в виде табл.12.
Таблица 12
|
Источник изменчивости |
Сумма квадратов |
ЧСС Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
Среднее |
F-отношение |
|
Между уровнями |
Sму |
p-1 |
|
Fр= |
|
Внутри уровней |
Sву |
N-p |
|
|
|
|
S0 |
N-1 |
|
|
Гипотеза Н0: а1=а2=…=ар=0 отвергается при выбранном уровне надежности (обычно, 95%), если Fр>FТ, где FТ – табличное значение F-распределения при ЧСС числителя и знаменателя p-1 и
N-p соответственно. При Fр£FТ делается вывод, что результаты наблюдений не противоречат гипотезе Н0.
Поможем написать любую работу на аналогичную тему