Совместность оценок дробного факторного эксперимента.

Дробный факторный эксперимент (ДФЭ)   Из-за показательного роста числа экспериментов с увеличением размерности пространства  ПФП оказываются практически неприемлемыми при больших . Однако из матрицы ПФП  может быть отобрана некоторая часть, называемая дробным факторным планом (ДФП), которая сохраняет свойство ортогональности. Правило построения ДФП состоит в следующем. Задается порядок дробности . Из  входных переменных отбирают n-p переменных (их называют основными), и для них строят полный факторный план . Этот план затем дополняют столбцами, соответствующими оставшимся переменным. Для определения способа образования этих столбцов вводится понятие генератора (генерирующего соотношения) плана. Генератор представляет собой произведение граничных значений () основных переменных, определяющее граничные значения элементов каждого из дополнительных столбцов матрицы плана. Так, для построения линейной модели от трех переменных  можно воспользоваться ДФП типа  с генератором :

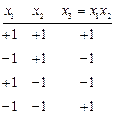
Чем выше размерность пространства , тем большее число генераторов плана можно предложить. Целесообразно выбирать такие из них, которые соответствуют незначимым взаимодействиям. Действительно, в состав базисных функций входят и левая и правая части генератора и, поскольку от эксперимента к эксперименту они меняются одинаковым образом, различить эффекты, соответствующие частям генератора, не представляется возможным. Так, если в качестве генератора выбрано соотношение , то получить раздельные оценки для и  нельзя. Соответствующий ДФП позволяет оценить лишь суммарное воздействие линейного фактора  и тройного взаимодействия . Подобные оценки называют смешанными. Однако, если взаимодействие незначимо, т.е. , то  будет практически несмешанной оценкой. Для определения порядка смешивания вводят понятие контраста плана. Контраст – это генерирующее соотношение, задающее элементы столбца свободного члена матрицы . (Со свободным членом уравнения регрессии связывается фиктивная переменная , тождественно равная единице.) Контраст получают из генерирующего соотношения умножением на переменную, стоящую слева от знака равенства. Для ДФП с генератором   контраст есть  , так как . Чтобы определить, с какими переменными или взаимодействиями смешана оценка некоторой данной переменной, необходимо умножить обе части контраста на эту переменную. При этом получают порядок смешивания оценок коэффициентов при использовании данного плана.

Пусть, к примеру, исследуется объект из трех переменных  полная модель которого есть

(В выражении (6.3) и далее случайное возмущение опускается.) В ходе исследования было решено ограничиться линейным (по переменным) описанием

,                                (6.4)

что дало основание воспользоваться ДФЭ  с генератором  с определяющим контрастом . Порядок смешивания для переменных  следующий:   ,  ,   .  (6.5)

С учетом (6.5) сгруппируем подобные члены в модели (6.3): . (6.6)

Сравнивая (6.6) и (6.4) , видим, что при оценивании линейной модели (6.4) получаются не чистые оценки свободного члена   и линейных эффектов  а оценки комбинаций, включающих двойные  и тройные (для свободного члена) эффекты:         .

Таким образом, платой за сокращение числа экспериментов стала совместность оценок. Если же поставить дополнительно четыре эксперимента с генератором , то получим оценки

.

Восемь оценок  дают возможность получить раздельные оценки эффектов. Так,  есть оценка , а – оценка  и так далее. Это и понятно, поскольку две серии экспериментов с генераторами   и  дают вкупе полный факторный эксперимент, который обеспечивает раздельное оценивание коэффициентов.

В отсутствии априорной информации о значимости взаимодействий предпочтение отдается генераторам, отвечающим взаимодействиям высокого порядка, поскольку коэффициенты регрессии при них по абсолютной величине, как правило, меньше.

К достоинствам факторных планов следует отнести их хорошие точностные свойства. Легко доказать, что они являются   D-, G-, A- оптимальными. К примеру, у ПФП , используемого для оценки коэффициентов модели вида , матрица плана X  и матрица значений базисных функций F имеют вид:     

,    .

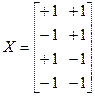Отсюда , а . Левая часть выражения (6.2) примет вид , поскольку . Максимум этой формы достигается в вершинах квадрата: ,  и равняется четырем. Число оцениваемых коэффициентов (k+1)  также четыре. Следовательно, условие (6.2) выполняется.