Экспериментальные методы одномерного поиска.

Рассматривается функция одной переменной y=f(x). Предпола-гается, что функция имеет только один экстремум (унимодальна); интервал поиска ограничен: ; значения выходной переменной неслучайны. Поиск осуществляется последовательно путем сравнения значений целевой функции в двух точках, выбираемых определенным образом. Эффективность E поиска характеризуется степенью локализации области экстремума после N экспериментов и выражается отношением длины начального интервала к остаточному , внутри которого находится экстремум целевой функции:       .

Далее для определенности будем полагать, что ищется максимум функции.

Эквидистантные планы Начальный отрезок делится на (N-1) равных частей, опыты проводятся при значениях:

.                  Поиск прекращается как только .

В зависимости от вида функции поиск прекращается при различных i, так что средняя эффективность составит E=(N–1)/2.

Метод деления отрезка пополам (метод последовательной дихотомии)

Эксперименты ставят парами в точках, отстоящих по обе стороны от середины отрезка. Координаты первой пары:

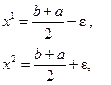 где e – малая величина.

Если , то максимальное значение надо ожидать на отрезке ; при на отрезке . Этот новый отрезок объявляется исходным, и далее процесс повторяется. Мера эффективности равна .

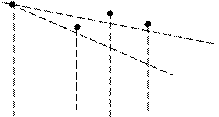
Заметим, что при наличии случайного компонента значение e не должно быть малым, что иллюстрируется рис.3.

                                                                           x

Рис. 3. Метод деления отрезка пополам

Если в точке х1 случайная компонента окажется отрицательной, а в точке х2 положительной, и значительной по величине в обеих точках, результаты сравнения значений отклика в этих точках направят поиск в противоположную сторону, Вот почему применение метода деления отрезка пополам в этих условиях становится проблематичным.

Поиск с использованием чисел Фибоначчи   Числа Фибоначчи задаются по следующим правилам:

,              

На первом шаге ставятся два эксперимента в точках x1=a+(b-a)q и x2=b-(b-a)q при q=FN-2/FN ,       (6.10)

где N выбирается заранее.

При  максимальное значение следует искать на отрезке , при – на отрезке . На последующих шагах ставят по одному эксперименту, меняя q по закону , где j – номер шага (j=2,3,…).

Легко показать, опираясь на определение чисел Фибоначчи,  что одна из координат, подсчитанная по формулам, аналогичным (6.10), будет совпадать с одной из предыдущих точек. Далее происходит сравнение значений функций в этих двух точках и процесс повторяется.          Мера эффективности метода составляет .

Так, при N=10 =144, а значит с помощью 11 экспериментов можно локализовать экстремум в области, не превышающей 1% размера начальной области поиска. Этот метод существенно эффективнее предыдущего. К его недостатку можно отнести необходимость заранее задавать число экспериментов.

Метод золотого сечения     Этот метод базируется на методе Фибоначчи и не требует предварительного задания числа экспериментов. В методе золотого сечения  вместо величины  на каждом шаге используется ее предельное значение при :                    .

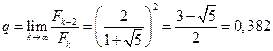Мера эффективности метода .