Свойства коэффициентов регрессии.

В практике эконометрического анализа чаще всего используют линейную парную регрессию (функциональная зависимость 1). Уравнение регрессии будем искать в виде . Неизвестные (пока) коэффициенты  являются оценками параметров . Можно сказать, что эмпирическое уравнение регрессии  является оценкой по выборке  регрессионной модели .

Метод наименьших квадратов для линейной парной регрессии состоит в следующем:

,

где  

Вычисляя производные по параметрам  и приравнивая их к нулю, приходим к следующей системе из двух уравнений

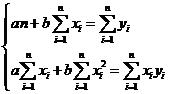
Решение системы уравнений называется оценкой неизвестных параметров по методу наименьших квадратов, его можно найти по формулам:

где

, , , .

Используя понятия выборочных дисперсий,  ковариаций и корреляций оценки наименьших квадратов (решение системы уравнений) можно записать специальным образом:

,   ,

где ,  —  выборочные средние,

 —  выборочные дисперсии,

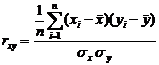 —  выборочный коэффициент корреляции.

Следовательно, парная эмпирическая линейная регрессия имеет вид

.

Нетрудно найти значения показателя, рассчитанные по линейной регрессии для тех значений объясняющего фактора, которые содержатся в выборке

,    

Особое значение для  проверки статистической значимости парной линейной регрессии имеют остатки (разности между значениями показателя, полученными в эксперименте, и вычисленными по уравнению линейной регрессии):

Вычисленному коэффициенту  при объясняющем факторе  в парной линейной регрессии можно дать естественную экономическую интерпретацию. Параметр b называется коэффициентом регрессии. Его величина показывает, насколько единиц изменится результат с изменением фактора на одну единицу.

Параметр a, вообще говоря, не имеет экономической интерпретации. Формально  – значение  при . Например, если a<0, то попытка его экономической интерпретации приводят к абсурду.

Зато можно интерпретировать знак при параметре а. Если, а>0, то относительное изменение результата происходит медленнее, чем изменение фактора.