Уравнение множественной регрессии в стандартизованном масштабе (назначение, формулы перехода к естественной форме)

Уравнение множественной регрессии  в стандартизованном масштабе:

,

где  - стандартизованные переменные

β - стандартизованные коэффициенты регрессии.

,  , для которых среднее значение равно нулю: , a среднее квадратическое отклонение равно единице: ;

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида:

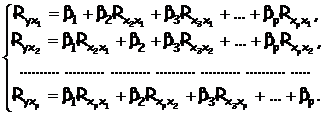
Решая его методом определителей, найдем параметры – стандартизованные коэффициенты регрессии (β - коэффициенты).

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится  в среднем результат, если соответствующий фактор хi изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии βi сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые не сравнимы между собой.

В парной зависимости стандартизованный коэффициент регрессии является линейным коэффициентом корреляции ryx. Подобно тому, как в парной зависимости стандартизованный коэффициент регрессии и корреляции связаны между собой, так и во множественной регрессии коэффициенты «чистой регрессии» bi связаны со стандартизованными коэффициентами регрессии βi, а именно:                

Это позволяет от уравнения регрессии в стандартизованном масштабе

переходить к уравнению регрессии в натуральном масштабе переменных:

.

Параметр а определяется как

.

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением βi.           

При двухфакторном анализе для уравнения регрессии в стандартизованном масштабе  β-коэффициенты могут быть определены с помощью коэффициентов частной корреляции по формулам:

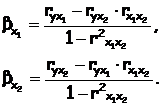
При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

,

мы преобразовываем ее в линейный вид

,

где переменные выражены в логарифмах.

Далее обработка МНК та же: строится система нормальных уравнений и определяется параметры lga, b1, b2,…, bp. Потенцируя значение lga, найдем параметр а и соответственно общий вид уравнения степенной функции.