УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНЫХ И РЕАЛЬНЫХ ЖИДКОСТЕЙ

УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНЫХ И РЕАЛЬНЫХ ЖИДКОСТЕЙ

1.     Простейшей механической моделью сплошной среды является модель идеальной жидкости, для которой характерно отсутствие сопротивления (сил трения) при скольжении одного слоя жидкости по другому. Отдельные части взаимодействуют только в виде нормального давления. Т.е. в любой точке идеальной жидкости касательные напряжения равны 0, а нормальные -(-р); (или через компоненты девиатора напряжений): .

Уравнением состояния дли идеальной жидкости служит зависимость плотности от давления и температуры:

 (2.1)

Например, для идеального газа приемлемо уравнение Клапейрона -Менделеева:

.

Если плотность жидкости - функция только давления r = f(p), то жидкость называют БАРОТРОПНОЙ.

Когда имеет место степенная зависимость r = срn, то говорят, что движение происходит при ПОЛИТРОПИЧЕСКОМ процессе.

Для капельных жидкостей, сжимаемость для которых чрезвычайно мала, в большом диапазоне изменения давления  связь между плотностью и давлением линейна:

,

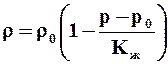r0 - плотность, соответствующая давлению р0, Кж - модуль объёмного сжатия, порядок которого равен 104nМПа.

Экспериментальные данные и общие физические представления показывают, что при больших температурах и давлениях любая среда практически обладает свойствами идеальной жидкости.

В нормальных условиях модель идеальной жидкости широко используется при изучении движения многих жидкостей и газов вдали от твёрдых границ.

Одно из наиболее известных уравнений движения идеальной жидкости - закон Бернулли:

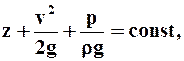
который гласит: При установившемся движении несжимаемой идеальной жидкости сумма геометрической, скоростной и пьезометрической высот вдоль линии тока остаётся величиной постоянной.

2.     В тех случаях, когда силами трения или напряжения сдвига при движении жидкости пренебречь нельзя, используют следующую по сложности модель - вязкую ньютоновскую жидкость. Уравнениями состояния для такой жидкости, кроме уравнения (2.1) , будет:

, (2.2)

Т.е. между компонентами девиатора напряжений и скоростей деформации существует прямо пропорциональная связь.

Или, через компоненты тензоров напряжений и скоростей деформации

Например, при плоском слоистом течении жидкости вдоль оси Ох1, когда v1 = v1(x1, x2), v2 = v3 = 0, нормальные и касательные напряжения равны:

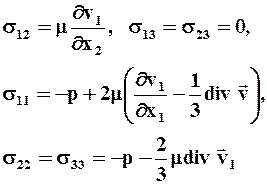
Если, кроме того, жидкость несжимаема (div v = 0) и скорость v1  не зависит от  x1 , то уравнение состояния имеет простейший вид:

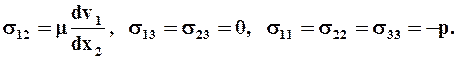
Коэффициент пропорциональности m называется КОЭФФИЦИЕНТОМ ВЯЗКОСТИ ИЛИ ДИНАМИЧЕСКОЙ ВЯЗКОСТЬЮ жидкости.

Размерность коэффициента динамической вязкости = = .

В системе СИ единицей вязкости является паскаль-секунда 1Па×с = 1н×с/м2.

Величина 1 пуаз = 0.1 Па× с.

Динамическая вязкость воды при 20°С равна 10-3 Па с.

Иногда пользуются отношением m/r, которое называется кинематической вязкостью  и обозначается буквой n. Размерность кинематической вязкости м2/с.

Для газов и капельных жидкостей динамическая и кинематическая вязкости слабо зависят от давления, но сильно от температуры: убывают с повышением температуры, а у воздуха - растут.

Таблица

Для учёта вязкости от температуры существует много различных эмпирических формул, однако практики предпочитают пользоваться табличными значениями.

Свойствами ньютоновских жидкостей, описываемых уравнениями (2.2), обладает большинство чистых жидкостей и газов. Однако, многие растворы, в том числе буровые и тампонажные, проявляют свойства, отличные от свойств ньютоновских жидкостей.

Вязкость неньютоновских жидкостей зависит не только от температуры и давления, но и от скорости сдвига, деформации, времени, характера движения.

3.     Основной признак неньютоновского поведения жидкостей заключается в нелинейном поведении компонент девиаторов напряжений и скоростей деформации.

 На рис.6 (Характерные зависимости напряжения сдвига от скорости деформации сдвига) показаны две характерные кривые зависимости напряжения сдвига s12 = t от скорости деформации сдвига 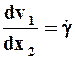 для неньютоновских жидкостей при плоском прямолинейном установившемся движении вдоль оси Ох1. Здесь же для сопоставления штрихпунктиром показана линейная зависимость для ньютоновской жидкости.

Поведение жидкости, описываемое кривой 1, называется ПСЕВДОПЛАСТИЧНЫМ, а кривой 2 - ДИЛАТАНТНЫМ. Различными авторами предлагалось множество аппроксимаций этих кривых, но наиболее широкое применение получили двухпараметрические аппроксимации:

Ø Модель Шведова-Бингама для псевдопластичных жидкостей (вязкопластичная бингамовская жидкость).

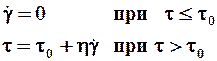.      (2.3)

Характеризуется тем, что обладает пространственной жёсткой структурой и благодаря этому сопротивляется внешнему воздействию до тех пор, пока вызванное им напряжение сдвига не превзойдёт предельного значения, соответствующего этой структуре. После этого структура полностью разрушается и жидкость начинает вести себя  как обачная ньютоновская вязкая жидкость при кажущемся напряжении, равном избытку действительного напряжения t над предельным t0 .

Ø Модель Освальда -Вейля (степенная), используемая для обоих типов жидкостей:

 (2.4)

где t0 - предельное (или динамическое) напряжение сдвига; h  - пластическая (структурная) вязкость; k - показатель консистенции; n - показатель неньютоновского поведения: при n <   1 жидкость псевдопластичная, при n >  1 - дилатантная.

Между параметрами моделей  устанавливается следующая связь:

где:  - скорость деформации сдвига, выше которой зависимость t от практически линейна (см. рис.6, стр.31).

ОТМЕТТЬТЕ ТОТ ФАКТ, что реологические параметры h,t0,k, n - для тампонажного и бурового растворов зависят от температуры, давления, состава, диапазона изменения скорости деформации сдвига , для которой справедливы модели (2.3) и (2.4).

4.     Чтобы установить характер зависимости между касательными напряжениями и скоростями деформации сдвига и определить реологические параметры жидкости в заданных условиях, используют наиболее простые формы движения:

Ø установившееся ламинарное (слоистое) течение жидкости вдоль оси цилиндрической трубы;

Ø тангенциальное течение между двумя соосными цилиндрами.

При этих течениях линии тока либо прямые линии, либо - концентрические окружности. Такие течения можно создать лишь в специальных приборах: капиллярных или ротационных вискозиметрах.

При течении жидкости между двумя вертикальными соосными цилиндрами длиной  L , из которых наружный вращается с угловой скоростью w, реологические параметры для бингамовской жидкости  могут быть определены из соотношения:

,

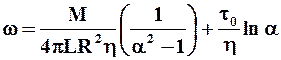а для жидкости, соответствующей степенной модели:

,

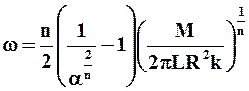где М -вращающий момент, приложенный к наружному цилиндру; a = R0/R; R0 и R - радиусы внутреннего и внешнего цилиндров соответственно.

Для произвольного течения несжимаемых (x = 0)вязкопластичных жидкостей используются следующие уравнения состояния, обобщающие уравнения (2.2) и модели (2.3), (2.4) :

lij = 0                                при  T £  t0

sij = 2 (h  +  t0 /H1)lij        при  T > t0      (2.5)

и                                    (2.6)

где Н1 - интенсивность скоростей деформаций сдвига при x  = 0:

,

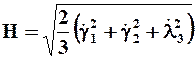Т - интенсивность касательных напряжений

     .

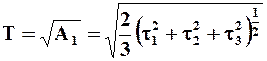При определённых нестационарных режимах течения буровые и тампонажные растворы могут проявлять особые свойства неньютоновского поведения:

Ø тиксотропность - зависимость жёсткости структуры от продолжительности деформирования и предыстории движения;

Ø запаздывание во времени установления деформации при действии постоянного напряжения или, наоборот, запаздывание во времени установления напряжений при постоянной деформации (релаксация напряжений).

5.     Эмпирически установлено, что по мере увеличения скорости течения всякое упорядоченное движение частиц жидкости постепенно нарушается и переходит в новую форму - турбулентное движение , при котором движение частиц становится неупорядоченным (хаотичным).  Несмотря на то, что первые наблюдения турбулентного течения были сделаны более 100 лет тому назад, до настоящего времени нет строгой теории, каким образом ламинарное движение перерождается в турбулентное. В 1883 году О. Рейнольдс впервые обнаружил, что переход ламинарного движения в турбулентное наступает при достижении некоторого критического значения параметра, который известен нам как параметр Рейнольдса: ,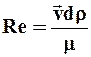

где   - средняя скорость потока;  d - диаметр трубы; r, m  - плотность и вязкость жидкости.

Для ньютоновских жидкостей наиболее вероятная нижняя граница = 2320, а верхняя » 50000. При этом, чем плавнее вход в трубу, тем позже наступает турбулентный режим. Помимо этого на величину верхней границы Reкр сильное влияние оказывают следующие факторы:

Ø сильное отклонение трубы от цилиндрической формы;

Ø заметная шероховатость поверхности трубы;

Ø наличие в жидкости твёрдых тел, коллоидных или дисперсных образований;

Ø изменение граничных условий;

Ø действие внешних возмущений и т.д.

Для вязкопластичных сред переход от структурного к турбулентному режиму течения принято определять по величине обобщённого параметра Рейнольдса:

Ø для степенной модели 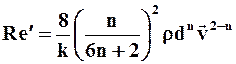  (2.8)

Ø для модели Бингама 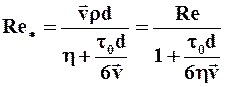   (2.9)

Нижняя граница обобщённых параметров Re¢ b Re* равна 2100.

Для количественного описания турбулентных течений Рейнольдс предложил действительные скорости  (давления) в данной точке представлять в виде суммы средних во времени величин и пульсационных составляющих. Однако, для развитого турбулентного течения пульсационные составляющие пренебрежимо малы со средними значениями величин, поэтому сохраняется интегральная теорема движения, эквивалентная трём дифференциальным уравнениям  (1.45) + уравнение неразрывности (1.13). В этом случае вместо обычных значений величин используются их средние значения, а вместо напряжений sij используется сумма компонент напряжений, связанных со средними скоростями + напряжения Рейнольдса: .

Иначе говоря, для решения задач турбулентного течения  ВОЗМОЖНО применение уравнений механики сплошной среды, при условии, что величины vi, p, sij  , входящие в эти уравнения, будут, соответственно, заменены на величины

Для описания напряжений Рейнольдса предложено несколько полуэмпирических уравнений состояния, наиболее известным из которых является уравнение Прандтля:

(2.10)

где l - коэффициент, характеризующий геометрическую структуру турбулентного потока, называемый путём смешения (перемешивания) или масштабом турбулентности, который зависит от расстояния до стенки канала.

В частном случае, при течении жидкости между параллельными плоскостями в направлении оси Ох1, уравнение (2.10) принимает вид:

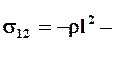
Анализируя свойства турбулентного потока в трубах вблизи твёрдой стенки, Прандтль принимал l = 0.36s, где s - расстояние от стенки трубы.

6.     Таким образом, ОБЩАЯ ЗАДАЧА ГИДРОМЕХАНИКИ заключается в определении:

Ø компонент vi (i=1,2,3)  вектора скорости `v ;

Ø компонент симметричного девиатора напряжений sij = sji (i,j = 1,2,3);

Ø давления р;

Ø плотности  r  жидкости в любой точке области.

В общем случае это 11 искомых функций, которые должны удовлетворять при ламинарном режиме течения полной системе дифференциальных уравнений:

Ø уравнение движения 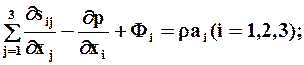     (2.11)

Ø уравнения неразрывности движения или сохранения массы

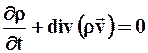 (2.12)

Ø уравнений механического состояния  r = f (p); (2.13)

Ø 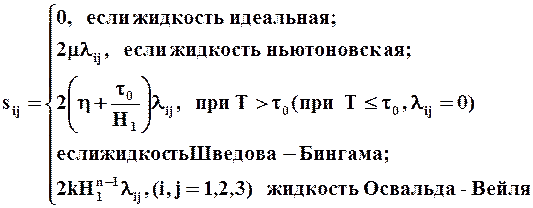(2.14)

Для неньютоновских жидкостей возможны и другие уравнения состояния. Известные в литературе уравнения Навье - Стокса можно получить, подставляя уравнения (2.14) в (2.11). При решении конкретных задач мы будем использовать упрощенный вид этих уравнений.

При турбулентных течениях жидкостей и газов внешний вид системы остаётся практически прежним, нужно только помнить, что вместо обычных величин в них подставляются величины усреднённые по времени и где напряжения Рейнольдса могут быть связаны с компонентами средних скоростей деформаций, например, посредством уравнения Прандтля (2.10)

обозначения основных величин

Ø компоненты девиаторов напряжений

Ø компоненты скоростей деформаций

Ø символ Кронекера

Ø соотношения Коши

Ø скорость деформации объёма

Ø проекции объёмных сил и ускорений

Ø интенсивность касательных напряжений

Ø интенсивность скорости деформации сдвига при   =0.

Решение системы уравнений может быть единственным и однозначным ТОЛЬКО при выполнении ГРАНИЧНЫХ УСЛОВИЙ:

Ø  - на поверхности контакта жидкость-твёрдое тело;

Ø р = р0  - на свободной поверхности (`v0,  p0 - заданные величины скорости твёрдого тела и внешнее давление).