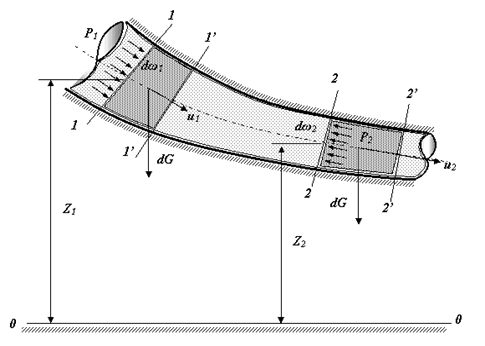
Рассмотрим установившееся течение элементарной струйки идеальной жидкости, на которую действуют только силы тяжести. Выберем два сечения 
и произвольную горизонтальную поверхность. Будем считать, что существует 
и 
, действует давление 
и 
, центры тяжестей сечений располагаются на высоте 
. Пусть за 
участок струйки сдвинулся и занял положение, ограниченное 
. Тогда 
. Следовательно, равны массы (
) и веса (
). Тогда изменение кинетической энергии всего жидкого тела будет определяться разностью кинетических энергий выделенных объёмов: 
. Работа сил тяжести: 
. Работа сил давления (работа положительной и отрицательной сил): 
. Выполнив следующие действия: 1) 
; 2) разделив каждый член уравнения на вес ; 3) приняв, что 
получим 
и 
– удельные энергии положения ж-ти в сечениях (нивелирные высоты); 
- удельные энергии давления (сжатия) жидкости в сечениях (пьезометрические высоты);
и 
- удельные потенциальные энергии жидкости в сечениях (гидростатические напоры);
и 
– удельные кинетические энергии жидкости в сечениях (скоростные напоры);
и 
– полные удельные энергии в каждом сечении струйки жидкости (полные напоры Н). Энергетический смысл уравнения Бернулли (1): в потоке идеальной жидкости её полная удельная энергия в сечении есть величина постоянная. (1) – закон сохранения энергии для струйки идеальной жидкости.
Поможем написать любую работу на аналогичную тему