Если поверхность имеет произвольную форму, то требуется находить 3 составляющих силы и 3 момента. Чаще рассматривают цилиндрические и сферические поверхности, имеющие вертикальную плоскость симметрии. Возьмем цилиндрическую поверхность (Рис. 14) с образующей, перпендикулярной плоскости рисунка и определим силу давления на эту поверхность в двух случаях:
– жидкость расположена сверху;
– жидкость расположена снизу.
На рисунке показана реакция стенки на жидкость, которая, как известно, равна силе давления жидкости на стенку (по третьему закону Ньютона). Рассмотрим условия равновесия объема жидкости ABDE, лежащей строго над интересующей нас криволинейной поверхностью. Условие равновесия в вертикальном направлении
Fв = p0Sг +G,
где Sг – горизонтальная проекция стенки;
G – вес жидкости в объеме ABDE.
Условие равновесия в горизонтальном направлении запишем с учетом того, что силы давления на площадки CD и AE равны:
![]()
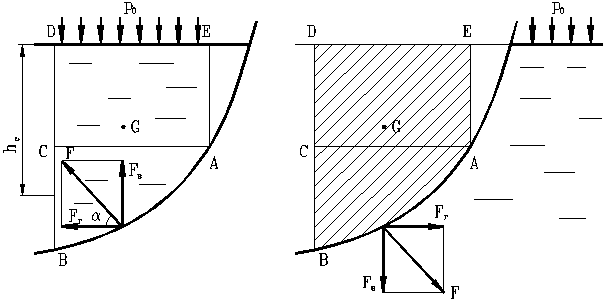
Рис. 14. Схема для определения силы давления жидкости
на цилиндрическую поверхность
Fг = (p0 + grhC)Sв.
По вычисленным составляющим Fг и Fв найдем величину силы давления жидкости на стенку
![]()
Направление силы давления на стенку определяет угол a
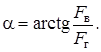
Для нахождения центра давления на цилиндрической стенке необходимо дополнительно определить положение центра масс объема ABDE, положение центра давления на вертикальную проекцию стенки. Центр давления находится из уравнения моментов. Если цилиндрическая поверхность круговая, то задача значительно упрощается, так как в этом случае равнодействующая силы давления жидкости на стенку проходит через ось цилиндрической поверхности. Дело в том, что в каждой точке поверхности давление направлено по нормали к стенке, то есть по радиусу и, таким образом, не создает момента относительно оси, проходящей через центр вращения. Тогда и равнодействующая сила не должна создавать момента относительно той же оси, то есть должна проходить через центр вращения.
В случае, когда жидкость находится ниже стенки, давления в каждой точке будут иметь те же значения, что и в первом случае, но направлены противоположно. Следовательно, определять силу давления на криволинейную стенку можно точно так же, но направлена она будет в противоположном направлении. Следует обратить внимание на то, что при определении вертикальной составляющей силы все равно надо вычислять вес жидкости в объеме ABDE, хотя на самом деле жидкости там нет.
Примененный сейчас прием определения вертикальной составляющей силы давления применим и для вывода закона Архимеда (Рис. 15).
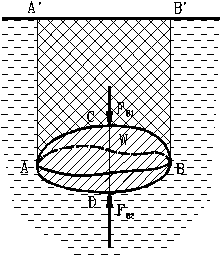
Рис. 15. Схема для доказательства закона Архимеда
Пусть в жидкость погружено тело произвольной формы объемом W. Возьмем проекцию этого тела на свободную поверхность жидкости и проведем вдоль полученной линии цилиндрическую поверхность с вертикальной образующей. Эта поверхность будет касаться тела по замкнутой линии, делящей поверхность тела на верхнюю и нижнюю части.
Найдем вертикальные составляющие силы давления жидкости на верхнюю и нижнюю части поверхности тела. Они будут равны весам жидкости соответственно в объемах ACBB’A’ и ADBB’A’. Обозначим их Fв1 и Fв2. Равнодействующая этих двух сил будет равна их разности, то есть весу жидкости в объеме тела, и направлена вверх.
Fa = Fв2 – Fв1 = grW.
Равнодействующая всех горизонтальных составляющих сил давления всегда равна 0, так как вертикальные проекции левой и правой, передней и задней частей тела всегда попарно равны, и противоположно направленные горизонтальные составляющие силы давления друг друга уравновешивают. Этот вывод можно получить и, не анализируя в тонкостях горизонтальные составляющие силы давления. Ведь если бы горизонтальная составляющая силы давления не была бы равна 0, то тело под ее действием поплыло бы в неподвижной жидкости, причем не затрачивая энергии. Это означало бы нарушение закона сохранения энергии.
Таким образом, мы доказали закон Архимеда, который гласит: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре масс объема погруженной части тела (центре водоизмещения).
Следует отметить, что центр масс тела и центр масс объема тела в общем случае не совпадают. Они совпадают только в случае, когда тело имеет равномерную плотность.
Если сила поддержания (архимедова) меньше веса тела, то оно тонет. Если больше, то тело всплывает на поверхность. Если равна, то тело плавает в толще жидкости.
Для равновесия плавающего тела необходимо, чтобы центр масс и центр водоизмещения лежали на одной вертикальной прямой. Если центр масс лежит ниже центра водоизмещения, то равновесие устойчивое, если выше, то – неустойчивое.
Поможем написать любую работу на аналогичную тему

