Уравнение постоянства расхода(неразрывности) для потока жидкости и газа.

Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме

Рассмотрим неподвижный объем в форме бесконечно малого параллелепипеда с ребрами dx, dy, dz и найдем массу входящей и выходящей жидкости.

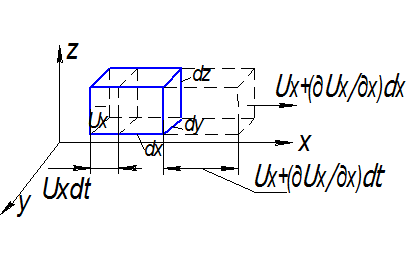
За малый промежуток времени dt через левую грань заходит объем жидкости:

dVл=Uxdtdydz,    (dydz-площадь)

входящая масса:                ,

(несжимаемая жидкость)

Объем входящей жидкости через правую грань за время dt:

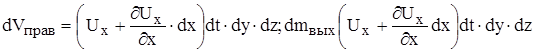
Изменение массы жидкости в объеме параллелепипеда за счет входа и выхода жидкости через левую и правую грани:

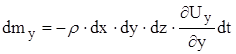
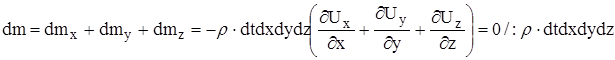
Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме:

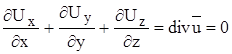
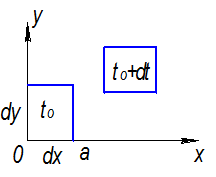
Рассмотрим изменение ребра оа за промежуток времени:

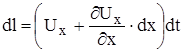-точка а перемещается на данную величину.

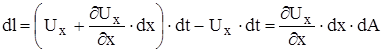- абсолютное изменение ребра                         за время dt

 -скорость изменения длины

-скорость изменения длины ребра dx (удлинение)

- относительная скорость деформации, удлинения ребра dx

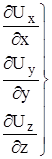-скорости относительных деформаций удлинений ребер параллелепипеда

(скорость объемной деформации, она должна=0)

Т.е. движение жидкости осуществляется так, что данная масса все время занимает один и тот же объем.

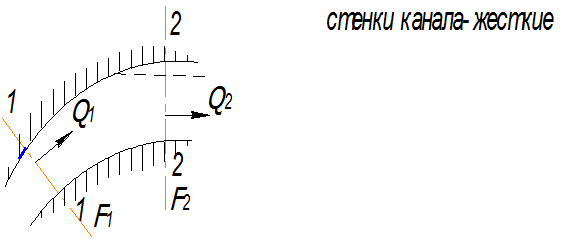Уравнение постоянства расхода.

1.     Предположим, что Q1>Q2.Это предположение неверно

2.     Q1<Q2(нарушается сплошность потока),неверно

3.     Q1=Q2 ; υ1F1= υ2F2 (расход постоянный) =соnst

Q1=Q2=υ1F1=υ2F2 – уравнение постоянства расхода для газов