Выбросы случайной функции за заданный уровень

Необходимость определения вероятностных характеристик процесса пересечения с. функцией заданного уровня возникает, когда необходимо вычислить вероятность того, что в течение срока службы нагрузка, действующая на строительную конструкцию, не превысит допустимого уровня. Найдем вероятность пересечения случайной функцией (дифференцируемой) X(t) некоторого уровня а в течение времени t. Полагая скорость изменения с.ф. V(t)=dX(t)/dt постоянной в течение времени dt (с точностью до бесконечно малых второго порядка) условие пересечения функцией X(t) уровня а за малый промежуток времени dt:

X(t)<a; X(t)+V(t)dt>a                                                            (74.5)

или

a-V(t)dt<X(t)<a (V(t)>0)                                                    (75.5).

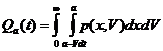                                                       (76.5),

где p(x,V) - совместная плотность распределения с.ф. X(t) и V(t).

Ввиду близости пределов внутреннего интеграла (его заменили на p(a,V)Vdt - площадь прямоугольника) вероятность выброса:

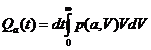                                                         (77.5).

Если разделить вероятность выброса Qa на время dt, в течение которого он ожидается, получится временная плотность вероятности выброса за уровень а в момент t (среднее число выбросов в единицу времени):

                                                             (78.5).

В случае стационарного с.п. X(t) и Y(t) - независимые с.ф. и (при том  и известна автокорреляционная функция для X(t) - KX(t)), следовательно,

p(x,V)=px(x)×pV(V),                                                              (79.5)

где p(x,V) - совместная плотность распределения X(t) и Y(t); px(x)×и pV(V) - соответственно плотности распределения X(t) и Y(t).

Тогда временная плотность вероятности выброса:

                                        (80.5),

где  - м.о. положительной скорости V(t).

Для нормального распределения X(t):

                                                      (81.5)

распределение скорости V(t) будет также нормальным и независимым от распределения X(t):                                                           (82.5).

М.о.  вследствие стационарности процесса. По (72) .

Подстановка (82) и (81) в (80) даст для временной плотности вероятности выброса

                                                   (83.5).

Доказательство (83.5):

.

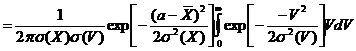Заменим подынтегральное выражение,

,

 тогда

,

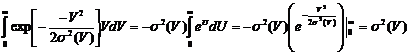и тогда .

Чем больше уровень а, тем меньше q(a). При очень малом значении q(a) выбросы можно рассматривать как редкие события, т.е. как независимые с.в.

Если число выбросов в течение времени t подчиняется закону Пуассона  (66), тогда вероятность того, что за время T не произойдет ни одного выброса при условии, что X(t) – стационарная функция

Pt=exp                                                                 (84.5)

Это функция надежности.

В случае нестационарной функции

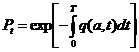                                                                   (85.5).