При последовательном соединении элементов разрушение происходит по наиболее слабому из них. Последовательным соединением элементов может быть названо также любое их соединение, образующее статически определимую систему. (Прочность – случайна, s – напряжение в стержне от фактической определенной нагрузки).
Интегральный закон распределения прочности i-того элемента системы – Pi(s) (т.е. вероятность того, что прочность элемента будет находиться на интервале (-¥,s), т.е. это вероятность разрушения). Вероятность неразрушения равна 1-Pi(s) для i-того элемента. Аналогично для всей системы ее вероятность не разрушения 1-Pc(s), где Pс(s) – интегральное распределение прочности всей системы, состоящей из n последовательно соединенных элементов. Согласно (3¢/2) и (4/2)
![]() (92.8)
(92.8)
|
Предполагается, что прочность каждого элемента является независимой с.в. Если все элементы имеют одинаковые распределения своей прочности, выраженной через внешнюю нагрузку (Pi(s)=P1(s), i =1,2,…,n), то вероятность не разрушения 1 - Pc(s) = n (93.8), где P1(s) – интегральное распределение прочности каждого элемента. Распределение плотности вероятности разрушения системы:pc(s)=nn-1×p1(s) (94.8), где p1(s) – плотность распределения прочности каждого элемента. Если прочность элементов подчиняется распределению Вейбулла (54.4) P1(s) = 1- exp(-csb) (95.8), то подставив (95.8) в (93.8) получим (вероятность разрушения системы) Pc(s) = 1- exp(-cnsb)=1 - exp(-cyb) (96.8), где
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
![]() (98.8),
(98.8),
где ![]() (в каждом стержне свое конкретное напряжение).
(в каждом стержне свое конкретное напряжение).
Здесь F – внешняя нагрузка;
si – напряжение, вызываемое усилием ![]() в i-том стержне;
в i-том стержне;
![]() - усилие в i-том элементе от внешней нагрузки F=1; Ai – площадь сечения i-того стержня.
- усилие в i-том элементе от внешней нагрузки F=1; Ai – площадь сечения i-того стержня.
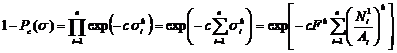 (99.8)
(99.8)
Тогда м.о. и стандарт прочности системы:
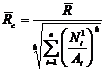 ,
, 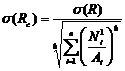 (100.8)
(100.8)
Пример.
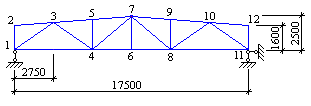
Дано: стальная статически определимая ферма. Нагрузка и размеры детерминированы, прочность всех стержней случайна, независима и распределена одинаково по нормальному закону. Сталь С245. Расчетное сопротивление Ry = 240 МПа, матожидание предела текучести ![]() МПа, стандарт предела текучести s(Ry) = 20 МПа. Тогда коэффициент вариации предела текучести
МПа, стандарт предела текучести s(Ry) = 20 МПа. Тогда коэффициент вариации предела текучести
![]() (7,7%).
(7,7%).
Функция распределения прочности элементов:
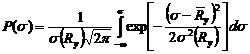 ,
,
где s - напряжение, действующее в стержне.
Значение P(s) – есть вероятность того, что случайный предел текучести Ry будет меньше действующего напряжения s, т.е. вероятность разрушения. Через интеграл вероятности Гаусса: ![]() определим вероятности разрушения каждого стержня:
определим вероятности разрушения каждого стержня:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
, ![]() .
.
|
Элемент |
Расчетное усилие, кН |
Унифицированное сечение |
Площадь А, см2 |
Напряжение s, МПа |
|
Вероятности разрушения |
|
|
ВП |
3-5 |
-316 |
2L100x7 |
25.6 |
-220.4 |
228 |
0.0239 |
|
5-7 |
-316 |
25.6 |
-220.4 |
0.0239 |
|||
|
НП |
1-4 |
232.2 |
2L75x5 |
14.78 |
157 |
0 |
|
|
4-6 |
313.2 |
14.78 |
212 |
0.0082 |
|||
|
Ст. |
4-5 |
-60.81 |
2L50x5 |
9.6 |
-141 |
0 |
|
|
Рас. |
1-3 |
-313.8 |
2L90x6 |
21.2 |
-221 |
0.0256 |
|
|
3-4 |
148.2 |
2L50x5 |
9.6 |
154.3 |
0 |
||
|
4-7 |
-30.7 |
2L63x5 |
12.26 |
-104.4 |
0 |
||
Тогда по (93.8) вероятность неразрушения фермы (надежность):
1 - Pc(r) = (1-0.0239)4×(1-0.0082)2×(1-0.0256)2=0.8478.
Ферма обладает такой надежностью в случае действия максимальных нагрузок, вероятность появления которых невелика, поэтому действительная надежность фермы больше. Кроме того, ферма не является в действительности статически определимой системой и появление в стержне напряжения равного пределу текучести не есть еще разрушение этого стержня.Поможем написать любую работу на аналогичную тему

