Нужна помощь в написании работы?
В действующих документах нормативные значения не совпадают с м.о. и сдвинуты по отношению к среднему значению.
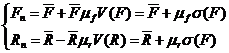 (11.1)(118),
(11.1)(118),
При коэффициенте изменчивости прочности менее 0,06-0,08 применяется нормальный закон распределения (т.е. не учитываются моменты высших порядков – асимметрия и эксцесс). Более всего это относится к стали, для бетона, каменной кладки, древесины и других материалов с коэффициентом изменчивости 0,15-0,25 и более корректнее использовать более точные законы распределения, учитывающие асимметрию и эксцесс. Например, функция распределения, полученная из распределения Пирсона III типа:
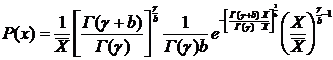 ,
где g и b – параметры.
,
где g и b – параметры.
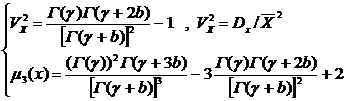 ,
асимметрия
,
асимметрия 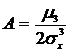 .
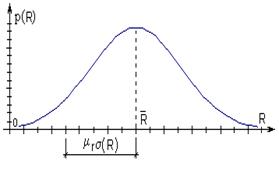
По СНиП II-23-81 ”Стальные конструкции. Нормы проектирования” (приложение 8а, стр. 92) при испытаниях металла нормативное значение предела текучести
.
По СНиП II-23-81 ”Стальные конструкции. Нормы проектирования” (приложение 8а, стр. 92) при испытаниях металла нормативное значение предела текучести 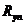 или временного сопротивления стали
или временного сопротивления стали 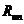 определяется по результатам статистической обработки:
определяется по результатам статистической обработки:
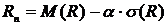 ,
где
,
где 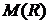 — математическое ожидание предела текучести или временного сопротивления;
— математическое ожидание предела текучести или временного сопротивления;
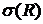 — среднеквадратическое отклонение предела текучести или временного сопротивления.
— среднеквадратическое отклонение предела текучести или временного сопротивления.
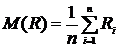 ;
(или по (19.3)
;
(или по (19.3)
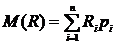 ,
где
,
где 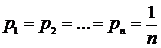 .
. 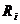 появляется один раз).
появляется один раз).
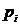 — вероятность появления возможных значений
— вероятность появления возможных значений 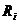 предела текучести или временного сопротивления;
предела текучести или временного сопротивления;
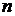 — число испытанных образцов (полная группа несовместных событий);
— число испытанных образцов (полная группа несовместных событий);
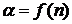 — коэффициент, учитывающий объем выборки.
— коэффициент, учитывающий объем выборки.
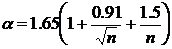 ,
при
,
при 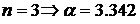 ;
;
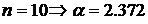 ;
;
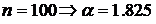 ;
;
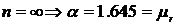 ,
,
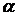 показывает, на какое число стандартов
показывает, на какое число стандартов 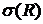 сдвинуто нормативное сопротивление по отношению к математическому ожиданию.
Чем больше
сдвинуто нормативное сопротивление по отношению к математическому ожиданию.
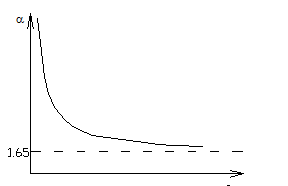
Чем больше 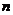 , тем достовернее полученные результаты, тем меньше
, тем достовернее полученные результаты, тем меньше 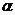 и больше
и больше 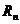 (
(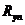 или
или  ).
).
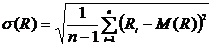 .
При значении коэффициента вариации (изменчивости)
.
При значении коэффициента вариации (изменчивости) 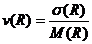 >0.1 использовать результаты, полученные из опытов, не допускается, т. к. они ненадежны. Кроме того, коэффициентом надежности по материалу
>0.1 использовать результаты, полученные из опытов, не допускается, т. к. они ненадежны. Кроме того, коэффициентом надежности по материалу 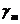 >1 учитывается разброс (изменчивость в неблагоприятную сторону) найденных нормативных сопротивлений.
Расчетное сопротивление вычисляется по формулам (здесь – для стальных конструкций):
>1 учитывается разброс (изменчивость в неблагоприятную сторону) найденных нормативных сопротивлений.
Расчетное сопротивление вычисляется по формулам (здесь – для стальных конструкций): 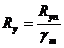 (по пределу текучести);
или
(по пределу текучести);
или 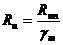 - по пределу прочности.
Нормативные значения принимаются с обеспеченностью 0.95, т. е. вероятность того, случайное фактическое сопротивление
- по пределу прочности.
Нормативные значения принимаются с обеспеченностью 0.95, т. е. вероятность того, случайное фактическое сопротивление 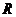 >
>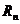 равна 0.95, т. е.
равна 0.95, т. е.
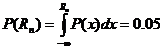 или, приняв нормальное распределение, через интеграл вероятности Гаусса Ф(х):
или, приняв нормальное распределение, через интеграл вероятности Гаусса Ф(х):
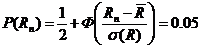 .
Определим математическое ожидание предела текучести для стали С235. Примем
.
Определим математическое ожидание предела текучести для стали С235. Примем  (худший вариант), и тогда
(худший вариант), и тогда
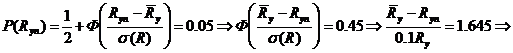
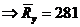 МПа при
МПа при 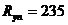 МПа.
При изменчивости
МПа.
При изменчивости 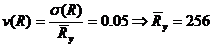 МПа.
Определим, насколько сдвинуто влево от математического ожидания предела текучести
МПа.
Определим, насколько сдвинуто влево от математического ожидания предела текучести 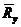 расчетное сопротивление по пределу текучести
расчетное сопротивление по пределу текучести 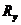 .
.
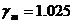 ;
;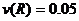 ;
;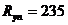 МПа;
МПа; 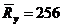 МПа;
МПа;
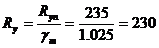 МПа;
МПа;
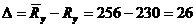 МПа;
МПа;
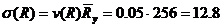 МПа.
Таким образом, расчетное сопротивление сдвинуто влево от математического ожидания предела текучести
МПа.
Таким образом, расчетное сопротивление сдвинуто влево от математического ожидания предела текучести 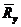 на
на 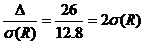 и вероятность того, что предел текучести будет меньше расчетного сопротивления
и вероятность того, что предел текучести будет меньше расчетного сопротивления 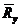 равна:
равна:
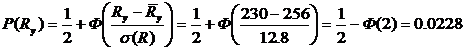 Обеспеченность расчетного сопротивления этой стали равна
Обеспеченность расчетного сопротивления этой стали равна
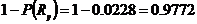 .
Нормами строго установлена обеспеченность расчетных сопротивлений только для древесины и древесных пластиков. Она составляет 0,99. Для бетонов, кирпича и других конструкционных материалов нет единой обеспеченности этой важнейшей прочностной характеристики, используемой при проектировании.
.
Нормами строго установлена обеспеченность расчетных сопротивлений только для древесины и древесных пластиков. Она составляет 0,99. Для бетонов, кирпича и других конструкционных материалов нет единой обеспеченности этой важнейшей прочностной характеристики, используемой при проектировании.
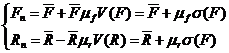 (11.1)(118),
(11.1)(118),
|
где |
|
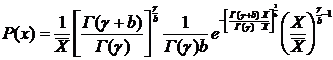 ,
где g и b – параметры.
,
где g и b – параметры.
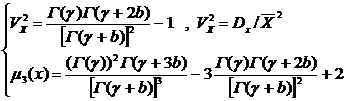 ,
асимметрия
,
асимметрия 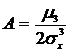 .
По СНиП II-23-81 ”Стальные конструкции. Нормы проектирования” (приложение 8а, стр. 92) при испытаниях металла нормативное значение предела текучести
.
По СНиП II-23-81 ”Стальные конструкции. Нормы проектирования” (приложение 8а, стр. 92) при испытаниях металла нормативное значение предела текучести Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

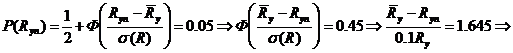
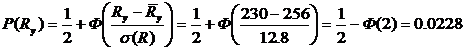 Обеспеченность расчетного сопротивления этой стали равна
Обеспеченность расчетного сопротивления этой стали равна
Поможем написать любую работу на аналогичную тему
Реферат
Статистический характер прочности. Начальная прочность материалов в строительных нормах
От 250 руб
Контрольная работа
Статистический характер прочности. Начальная прочность материалов в строительных нормах
От 250 руб
Курсовая работа
Статистический характер прочности. Начальная прочность материалов в строительных нормах
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
