В большинстве случаев нагрузки, действующие на строительные конструкции, представляют собой случайные функции Q(t). Случайная функция Q(t) характеризуется математическим ожиданием ![]() (детерминированная функция аргумента t) и корреляционной функцией Kx(t1,t2) (см (67)).
(детерминированная функция аргумента t) и корреляционной функцией Kx(t1,t2) (см (67)).
Обычно нагрузка Q(t) — стационарный (или квазистационарный) случайный процесс и случайная функция.
Вернемся к формуле временной плотности вероятности выброса за уровень а для случайного стационарного процесса, т. е. когда случайная функция X(t) независима со своей скоростью изменения ![]() и тогда случайные функции X(t) и V(t) можно заменить случайными величинами X и V с плотностями распределения
и тогда случайные функции X(t) и V(t) можно заменить случайными величинами X и V с плотностями распределения ![]() и
и![]() .
.
![]() (14.12)
(14.12)
Применительно к перегрузкам, т. е. превышению нагрузки Q(t) или комбинации нескольких нагрузок некоторого допустимого уровня нагрузки а, запишем (аналогично (14.12)):
![]() ,
,
где u(a) назовем интенсивностью отказов конструкции, считая отказом превышение нагрузкой Q(t) допускаемого для данной конструкции значения;
![]() и
и ![]() — плотности распределения Q(t) с аргументом а и V(t).
— плотности распределения Q(t) с аргументом а и V(t).
Величина, обратная интенсивности отказов, — период отказа, т. е. средняя продолжительность интервала между соседними выбросами (отказами).
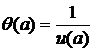
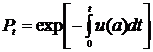 ,
где
,
где 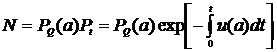 , (15.12)
, (15.12)Поможем написать любую работу на аналогичную тему

