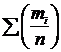Определение  характеристик распределения по  экспериментальным  данным. Статистические ряды

В статистике используются понятия генеральной совокупности и выборки. Пример генеральной совокупности - данные о прочности какой-либо марки стали по ВСЕМ металлургическим заводам страны. Обычно оперируют с частью генеральной совокупности, отобранной для анализа - ВЫБОРКОЙ. Пример выборки - данные о весе снежного покрова за ряд лет по одной метеостанции.

Упорядоченные по величине результаты опытов или наблюдений (например, расположенные в порядке возрастания значений) называют ВАРИАЦИОННЫМ РЯДОМ. Результаты проведенных наблюдений образуют ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ.

Разность наибольшего и наименьшего членов ряда R = Xn - X1 называется РАЗМАХОМ эмпирического распределения, а число наблюдений n - объемом выборки.

Функцией распределения случайной величины для данного статистического материала (ВЫБОРКИ) будет частота события < X, где X - любое возможное значение случайной величины .

Значение статистической функции распределения легко вычислить, подсчитав число опытов m, в которых величина приняла значение, меньшее, чем X, и разделив его на общее число произведенных опытов n.   

                                                             (2.20)

Вместо зависимости (2.20) часто используют зависимость

,                                                          (2.21)

дающую средние значения частот. Эта зависимость хороша для значений случайной величины , близких к средним, однако, в области крайних значений (m0, mn) она дает искаженные результаты.

Имеются и другие предложения, например

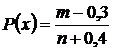                                                       (2.22)

Эта зависимость определяет МЕДИАНЫ  частот распределения.

    P(X)

0        X1                                                                               Хn                X

При большом числе наблюдений с простой статистической совокупностью становится работать неудобно. В этом случае на основе обработки строится СТАТИСТИЧЕСКИЙ РЯД.

Диапазон наблюдений значений величины  делят на интервалы (разряды). Определяется количество попаданий значений в каждый интервал.

Обычно число интервалов выбирают в пределах 10 - 15, при малых объемах выборки 5-6. Однако во многих случаях для анализа больших выборок число интервалов увеличивают. В монографии Л. П. Пилюгина , где оценивается надежность строительных конструкций на основе метода преобразования рядов распределения, число интервалов выбирается в пределах 20 - 25. Если значение попадает на границу интервалов, то его можно отнести к обоим интервалам, прибавив к числу попаданий m того и другого разрядов по 1/2.

Ниже в таблице обработаны результаты испытаний чистых стандартных образцов древесины сосны на сжатие. По табличным значениям построена гистограмма распределения предела прочности, ступени которой напоминают график кривой плотности нормального закона распределения Гаусса.

Таблица              Обработка результатов испытаний древесины сосны на сжатие

|

0,25-                                                      =====

|                                                     |           |

|                                                     |           =====

|                                                     |           |         |

|                                           =====           |         |

|                                           |         |           |         =====

|                                           |         |           |         |         |

|                                           |         |           |         |         ====

|                                 =====         |           |         |         |         |

|                                 |         |         |           |         |         |         |

|                       =====         |         |           |         |         |         =====

|             =====         |         |         |           |         |         |         |         |

|             |         |         |         |         |           |         |         |         |         =====

-----------------------------------------------------------------------------------------------

  35      37     39      41      43        45      47      49      51        53        55

                          σmax, МПа

        35      37       39      41       43     45      47       49      51     53       55         σmax, МПа

По данным этой же таблицы можно построить график суммы частот попадания в соответствующие интервалы, соответствующий интегральному закону распределения предела прочности древесины для данной выборки, называемый эмпирической функцией распределения.

Числовые характеристики - МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЮ эмпирического распределения обычно определяют по приближенным формулам:

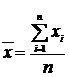
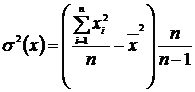                                         (2.23)