Расчетное сопротивление

Частное от деления нормативного сопротивления на коэффициент надежности по материалу есть расчетное сопротивление, используемое в расчетах по 1-й группе предельных состояний.

Обеспеченность расчетного сопротивления нормами проектирования или стандартами не установлена, за исключением конструкций из дерева и пластиков. При нормировании расчетных сопротивлений учитываются многочисленные факторы разных типов, причем, статистическая оценка многих из них весьма затруднительна (например, влияние концентрации напряжений у дефектов структуры древесины или бетона).

В таких случаях учтен эмпирический опыт предыдущего безаварийного проектирования и строительства. В связи с этим можно заключить, что обеспеченность расчетных сопротивлений даже одного и того же материала при разных видах напряженного состояния различна, не говоря уже о разных видах конструкционных материалов. Во всяком случае, она значительно выше обеспеченности нормативного сопротивления. Несложно вычислить ее для конструкционной или арматурной стали.

Считается, что для большинства материалов обеспеченность расчетного сопротивления не ниже 0,99 (для древесных плит ДВП, ДСП, ЦСП). В большинстве случаев она значительно выше и может достигать значения 0,999. Нужно также учитывать, что в СНиПах приведены округленные значения прочностных и деформационных характеристик. Это в определенной степени влияет на обеспеченность расчетных значений.

ПРИМЕР 1  Определить обеспеченность расчетного сопротивления изгибу древесно-стружечных плит со следующими характеристиками (табл. 12 Пособия по проектированию ДК).

Rн = 16 МПа, R = 5,76 МПа, коэффициент вариации v = 0,16, коэффициент длительного сопротивления mдл = 0,53, масштабный коэффициент kp = 0,8.

РЕШЕНИЕ:

Коэффициент надежности по материалу вычислим из соотношения между нормативным и расчетным сопротивлением с учетом того, что масштабный эффект и различие длительной и кратковременной прочности учитываются отдельными коэффициентами, которые будем считать детерминированными.

Из соотношений расчетного и нормативного сопротивлений для древесины и древесных пластиков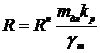

отсюда

 =

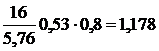
Выразим нормативное сопротивление через временное с учетом того, что обеспеченность его 0,95:

Rн  = Rср(1 - 1,645v)

где коэффициент 1,645 определяет обеспеченность 0,95.

В свою очередь так же можно выразить расчетное сопротивление

R = Rср(1 - tv),

где  t   определяет неизвестную обеспеченность.

Из этих соотношений

и отсюда

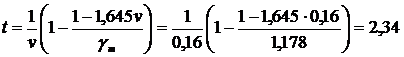
По таблице I находим, что такой коэффициент соответствует значению интеграла вероятностей Ф(t) = 0,490.

Тогда вероятность непревышения расчетного сопротивления составляет

0,5 - Ф(t) = 0,50 - 0,49 = 0,01,

что соответствует обеспеченности  P = 1 - 0,01 = 0,99.

Именно такое значение обеспеченности приведено для древесных плит в п. 3.15 Пособия по проектированию деревянных конструкций.

Решим эту же задачу для случая действия только кратковременной нагрузки малой продолжительности, соизмеримой с длительностью стандартных испытаний (например, при сейсмической нагрузке), когда mдл = 1. Тогда

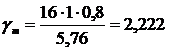
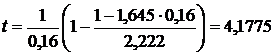
Ф(t) = 0,499985;

0,5 - Ф(t) = 1,5*105.

Обеспеченность в этом случае составляет P = 1 - 1,5*105  = 0,999985

Таким образом, при совместном действии длительной и кратковременной (снеговой) нагрузок в течение примерно 2 месяца может разрушиться 1 образец древесных плит из 100, а при кратковременном нагружении до напряжений  σ = Rн - только 15 образцов из 1000000 (МИЛЛИОНА) или 1 из 66667.