Статистическое распределение скоростей ветра

Для описания распределения скоростей ветра метеорологи рекомендуют распределение Вейбулла

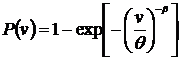                                                         (9.15)

где P(v) -  вероятность того, что скорость ветра не превысит значения v;

θ и β - коэффициенты, определяемые для каждой метеостанции и зависящие от ветрового режима данной местности.

Для района Москвы, например, получены значения θ = 4,42  и β = - 0,15.

Для описания распределения годичных или месячных максимумов скорости ветра используется, как и для максимумов снеговой нагрузки, двойное экспоненциальное распределение Гумбеля

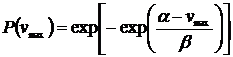                                        (10.15)

В табл. 4.15 приведены статистические характеристики ветрового давления для семи ветровых районов, вычисленные с использованием двойного экспоненциального распределения. Из этой таблицы хорошо видно, что нормативное значение ветрового давления, установленное в СНиП 2.01.07-85*, весьма близко к математическому ожиданию. Таким образом, в вероятностных расчетах, где используются не нормативные или расчетные значения нагрузок, а математические ожидания и коэффициенты вариации, для ветровой нагрузки можно использовать приведенные в нормах значения  для соответствующего ветрового района.

Таблица 4.15  Статистические характеристики ветрового давления