Строгое определение понятия адсорбции по Дж.Гиббсу: адсорбцией данного компонента на границе раздела двух фаз называется разность между фактическим количеством этого компонента в системе и тем его количеством, которое было бы в системе, если бы концентрации в обеих сосуществующих фазах были постоянны вплоть до некоторой геометрической поверхности, разделяющей их.
Эта разность может быть положительной или отрицательной. Она обозначается символом G (гамма) и имеет размерность моль/м2. Эту величину называют избыточной адсорбцией по Дж. Гиббсу.
Хотя в приведенном определении адсорбция отнесена к геометрической поверхности, не имеющей толщины (что удобно при выводе уравнений), фактически граница между фазами представляет собой очень тонкий слой (поверхностный слой), в котором все свойства отличаются от свойств объемных фаз и изменяются не скачкообразно, а непрерывно.
На рис. 13.1 показано возможное изменение концентрации вблизи границы раздела: концентрация компонента может быть как выше концентраций в обеих фазах (1), так и ниже (2) или иметь промежуточное значение. Эта область может рассматриваться как поверхностный слой. Таким образом, изучая границу раздела фаз, нужно рассматривать состояние трех фаз: двух объемных и одной поверхностной.
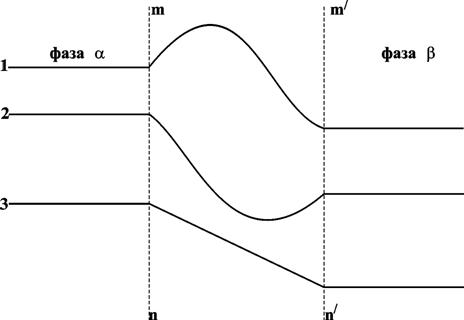
Рис. 13.1. Изменение концентрации компонентов у границы раздела фаз;
поверхностный слой – mn-m’n’
Уравнение, устанавливающее связь между всеми параметрами процесса адсорбции – величиной поверхностного натяжения s, концентрацией компонента в одной из фаз, его адсорбцией Г, было выведено Дж. Гиббсом в 1876 г. Это уравнение является общим термодинамическим уравнением, справедливым для любых составов и природы поверхности раздела фаз.
Рассмотрим систему, состоящую из двух компонентов 1 и 2 и двух фаз a и b, разделенных поверхностью раздела с площадью S. Общее число молей каждого компонента в системе равно n1o и n2o. Если считать, что поверхностный слой не имеет толщины, т.е. представляет собой геометрическую поверхность, то обе объемные фазы будут иметь постоянный состав вплоть до этой геометрической поверхности. Обозначим число молей каждого компонента в каждой из этих фаз соответственно через n1a,n1b ; n2a,n2b. Так как на поверхности имеет место адсорбция, то, очевидно, n1o ¹ n1a + n1b и n2o ¹ n2a + n2b.
По вышеприведенному определению адсорбция каждого компонента Г1 и Г2 , отнесенная к единице площади поверхности, равна
![]() . (13.1)
. (13.1)
Чтобы найти Г1 и Г2, напишем уравнение энергии Гиббса для двух фаз a и b в отдельности и для всей системы в целом. В последнем случае, очевидно, нужно включить в уравнение член sdS:
dGa = - Sa dT + VadP + m1dn1a + m2dn2a;
dGa = - Sb dT + VbdP + m1dn1b + m2dn2b;
dGo = - So dT + VodP + sdS + m1dn1o + m2dn2o. (13.2)
Укажем на уравнение Гиббса-Дюгема, которое устанавливает связь между химическими потенциалами:
dG = - S dT + VdP + Smidn1 (P, T – постоянные). (13.3)
Тогда для бинарной системы получим
dG = m1dn1 + m2dn2. (13.4)
Интегрируя это уравнение при постоянных значениях m1 и m2, получим
G = m1n1 + m2n2. (13.5)
Следовательно,
dG = m1dn1 + m2dn2 + n1dm1 + n2dm2. (13.6)
Из (13.4) и (13.6) вытекает, что
![]() . (13.7)
. (13.7)
Это уравнение носит название уравнения Гиббса-Дюгема и связывает изменение химических потенциалов компонентов. Тогда с учетом уравнения Гиббса-Дюгема и поверхностных явлений получаем:
n1adm1 + n2adm2 = 0;
n1bdm1 + n2bdm2 = 0; (13.8)
Sds +n1odm1 + n2odm2 = 0.
Сложение двух первых уравнений и вычитание полученной суммы из третьего дает
![]() . (13.9)
. (13.9)
В качестве примера рассмотрим две конкретные системы: двухкомпонентный жидкий раствор, находящийся в равновесии со своим двухкомпонентным насыщенным паром, и твердое тело, находящееся в равновесии с однокомпонентным газом, совершенно не растворимым в этом твердом теле.
Поскольку в первом случае точное положение разделяющей геометрической поверхности несколько условно, то можно выбрать положение ее, при котором
Г1 = 0,
тогда
ds = - Г2dm2. (13.10)
Во втором случае вследствие нерастворимости газа в объеме твердого тела, объемные свойства этого тела, в частности его химический потенциал, не изменяются при адсорбции. Приписывая твердому телу индекс 1, имеем:
m1 = const и dm1 = 0,
поэтому
ds = - Г2dm2. (13.11)
В обоих случаях получено одно и то же уравнение. Поэтому можно считать, что адсорбционное уравнение Гиббса имеет вид:
ds = Г2dm2. (13.12)
Оно является основным в учении о поверхностных явлениях.
Рассмотрим далее реальный раствор. Для реального раствора
m = mо(Т) + Rtlna,
где а – активность, тогда:
dm = RТ d lna.
Подставив это значение в уравнение (13.12), получим:
ds = - Г Rt d lna,
или
![]() . (13.13)
. (13.13)
В разбавленных растворах а » С (где С – концентрация)
![]() , (13.14)
, (13.14)
а для идеального или разреженного идеального газа
![]() . (13.15)
. (13.15)
Уравнение (13.14) показывает, что если при адсорбции поверхностное натяжение s уменьшается с ростом концентрации С, т.е. ds/dC < 0, то адсорбция Г – положительна. Это соответствует поверхностно-активным веществам. Наоборот, если s растет с ростом С, то ds/dC > 0 и Г – отрицательно. Это соответствует поверхностно-инактивным веществам. Если известна зависимость s от С (т.е. изотерма поверхностного натяжения s = f(C) , то по уравнению Гиббса можно для каждого значения концентрации найти ds/dC и по уравнению Гиббса вычислить значение Г, т.е. построить изотерму адсорбции.
Поможем написать любую работу на аналогичную тему

