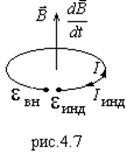
Рассмотрим энергию магнитного поля контура с током (рис.4.7). В начальный момент времени 
.
Увеличение тока в витке приведет к изменению (возрастанию) потока магнитного поля через контур и возникновению ЭДС индукции, направленной против внешней ЭДС. Чтобы достичь установившегося значения тока 
, источник внешней ЭДС совершает работу против ЭДС индукции:
; (4.29)
- заряд, прошедший за время 
по контуру. Работа идет на увеличение энергии магнитного поля. Тогда:
, (4.30)
и с учетом 
выражение (4.30) перепишется как:
. (4.31)
Интегрируя (4.31), получаем энергию магнитного поля, создаваемого током в контуре с индуктивностью 
:
. (4.32)
Для произвольного числа витков работа внешней ЭДС в k-м витке:
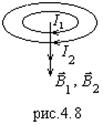
, (4.33)
при этом нужно учесть, что изменение потока может происходить не только за счет тока в этом контуре, но и за счет тока, текущего в другом (соседнем) контуре (он тоже создает магнитное поле).
Так, для двух витков с токами 
и 
и площадями сечения 
и 
(рис.4.8) можно записать:
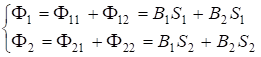. (4.34)
Кроме того:
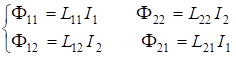, (4.35)
здесь 
и 
- коэффициенты самоиндукции; 
и 
- коэффициенты взаимной индукции.
Докажем, что 
на примере бесконечно длинного соленоида с двумя обмотками. Индукция магнитного поля в одной обмотке 
, в другой 
. Считаем, что объем у обмоток одинаков 
; т.к. 
, то:
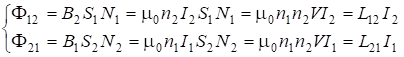. (4.36)
Из системы (4.36) следует, что:
. (4.37)
Тогда в общем случае 
, изменение потока в k – той обмотке:
.
По (4.33) работа внешней ЭДС в k – том витке:
Тогда из 
,
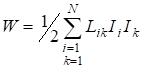‑ (4.38)
энергия магнитного поля, создаваемого токами 
и 
. Энергия локализована на токах, создающих магнитное поле.
Теперь рассмотрим энергию магнитного поля при наличии магнетиков на примере соленоида, имеющего 
витков с током , внутрь которого помещен магнетик с проницаемостью 
.
По теореме о циркуляции для вектора 
(4.21) получим: 
т.е.
. (4.39)
Тогда 
, 
, где объем 
выражен через сечение и длину соленоида. По формуле (4.32), считая, что - индуктивность соленоида, получаем:
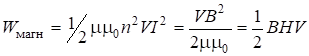. (4.40)
Из (4.40) следует, что плотность энергии магнитного поля в среде:
(4.41)
и энергия локализована на поле независимо от того, как оно создано. Для электрического поля в среде: 
.
Для сравнения с плотностью энергии магнитного поля в вакууме запишем формулу (4.41) в виде:
Если 
(вакуум), то 
. Сравнение показывает, что плотность энергии поля в среде больше, чем вакууме.
Теперь рассмотрим энергию магнитного поля при наличии магнетиков на примере соленоида, имеющего витков с током , внутрь которого помещен магнетик с проницаемостью .
По теореме о циркуляции для вектора (4.21)получим: т.е.
(4.39).
Тогда , , где объем выражен через сечение и длину соленоида. По формуле (4.32), считая, что - индуктивность соленоида, получаем:
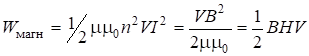. (4.40)
Из (4.40) следует, что плотность энергии магнитного поля в среде:
, (4.41)
и энергия локализована на поле независимо от того, как оно создано.
Для электрического поля в среде: .
Для сравнения с плотностью энергии поля в вакууме запишем формулу (4.41) в виде:
Если (вакуум), то . Сравнение показывает, что плотность энергии поля в среде больше, чем вакууме.
Поможем написать любую работу на аналогичную тему