Рассмотрим однородное магнитное поле, которое пересекается плоскостью.
А) n - нормаль к плоскости Угол между векторами В и n.
Тогда магнитным потоком через поверхность является произведение
В вектора магнитной индукции на площадь данной поверхности.
![]()
Единицы измерения =Вб=Тл м2.
Б) Магнитное поле через произвольную поверхность.
Разбиваем поверхность на дифференциально малые участки. Каждый из которых можно рассматривать как элемент плоскости.
![]()
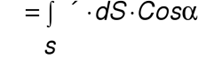
Важное свойство магнитных полей, связанное с магнитным потоком выражается теоремой Остроградского-Гаусса.
Теорема: Магнитный поток через любую замкнутую поверхность всегда равен нулю.
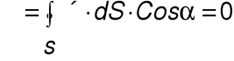
Рассмотрим эту теорему без доказательства, но проанализируем ее следствия:
1. Из теоремы следует, что в магнитном поле нет аналога электрического заряда, т.е. нет магнитных монополий (т.е. любая частица вещества имеет и северный полюс и южный и они неотделимы).
2. Магнитные силовые линии должны быть замкнутыми (не имеют начала и конца).
3. Из теоремы видно, что какое количество потока втекает внутрь замкнутой поверхности такое же количество и вытекает.
Поможем написать любую работу на аналогичную тему

