Работы перемещения проводника и контура с током в магнитном поле

На проводник с током в МП действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки), то под действием  он будет в МП перемещаться. Следовательно, МП совершает работу по перемещению проводника с током.

1. Для определения этой работы рассмотрим проводник длиной lс током I (он может свободно перемещаться), помещенный в однородное м.п. перпендикулярное к плоскости контура. Направление силы определяется по правилу левой руки, а значение – по закону Ампера.

Под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая МП равна:

т.к.

– площадь, пересекаемая проводником при его перемещении в магнитном поле.

Поток вектора магнитной индукции, пронизывающей эту площадь равен:

Таким образом, работа по перемещению проводника с током в МП, равна произведению силы тока на магнитный поток, пересеченный движущимся проводником:

Полученная формула справедлива и для произвольного направления вектора .

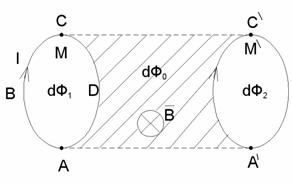
2. Вычислим работу по перемещению замкнутого контура с постоянным током в м.п. (произвольное движение). Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение . Направление тока в контуре – по часовой стрелке и м.п. перпендикулярно плоскости чертежа.

Контур М мысленно разобьем на два соединенных своими концами проводника: АВС и СDА. Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в м.п., равна алгебраической сумме работ по перемещению проводников АВС и СDА (dA1 и dA2), то есть:

Силы приложенные к участку CDA контура образуют с направлением перемещения острые углы, поэтому совершаемая ими работа dA2>0. Эта работа, согласно формулам равна:

где dФ0 – поток, который пересекает проводник CDA при движении; dФ2 – поток, пронизывающий контур в его конечном положении.

Силы, действующие на участок АВС контура, образуют с направлением перемещения тупые углы, следовательно dA1 <0. Проводник АВС пересекает при своем движении поток dФ0 сквозь поверхность и dФ1 – поток, пронизывающий контур в начальном положении.

Следовательно:

Подставляя выражения для dA1 и dA2 в формулу (37.5), получим выражение для элементарной работы:

где

– изменение магнитного потока сквозь площадь, ограниченную контуром с током.

Таким образом,

Проинтегрировав это выражение, определим работу, совершаемую силами Ампера при конечном произвольном перемещении контура в м.п.: