Энергия магнитного поля. Объемная плотность энергии

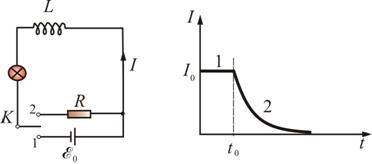
Рис. 5.6

      Сначала замкнем соленоид L на источник ЭДС  , в нем будет протекать ток  . Затем в момент времени   переключим ключ в положение 2 – замкнем соленоид на сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа:   ,  или

      Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией

      Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:

 .

 ; отсюда 

      Подставим эти значения в формулу (5.5.3):

      Обозначим w – плотность энергии, или энергия в объеме V, тогда

      но т.к.  , то

      Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле

а плотность энергии

      Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:

 ,   отсюда      .

      Т.к. в вакууме  , имеем

Объемная плотность энергии магнитного поля вычисляется по формуле:

wм=B22μμ0,wм=B22μμ0,

где BB −− магнитная индукция, μμ −− магнитная проницаемость, μ0=4π⋅10−7 Гн/мμ0=4π⋅10−7 Гн/м −−магнитная постоянная.

Формула для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Магнитная энергия локализована в самом магнитном поле.

В однородном магнитном поле в объеме ΔVΔV содержится энергия:

ΔW=wм⋅ΔV.ΔW=wм⋅ΔV.

Энергия произвольного магнитного поля может быть найдена путем интегрирования объемной плотности wэwэ по всему объему, в котором создано магнитное поле.