Используя определение коммутатора показать, что выполняются тождества:
а) 
;
б) 
.
Решение.
а) По определению коммутатора:
б) По определению коммутатора раскроем скобки слева, а потом справа:
- слева;
- справа.
Т.о. 
.
Показать, что произвольный оператор может быть представлен в виде суммы эрмитовой и антиэрмитовой частей.
Решение.
Представим некий оператор 
в следующем виде:
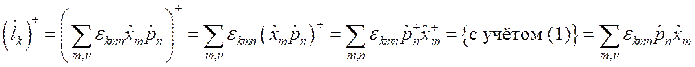, где символ «
» - эрмитово сопряжение.
Далее отдельно сформируем следующие част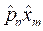и:
и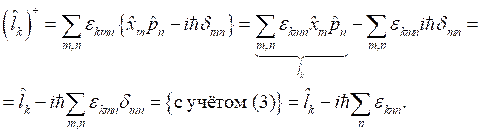 
.
Чтобы утверждать, что 
и 
- требуемые части, необходимо проверить выполнение условия эрмитовости операторов, а именно: 
и 
. Таким образом:
;
.
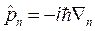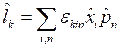Т.о. 
, где и - эрмитова и антиэрмитова части соответственно.
Используя условие сопряжения показать справедливость следующего равенства:
.
Решение.
Условие сопряжения выглядит следующим образом:
, откуда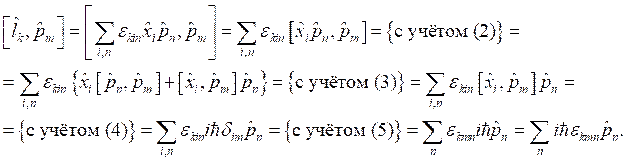 
.
С помощью этого свойства проведём следующее преобразование:
.
.
Т.о. .
Заметим, что это выражение выполняется при равенстве:
- что и требовалось показать.
Показать, что собственные значения унитарного оператора по модулю равны единице.
Решение.
По определению унитарного оператора:
.
Запишем скалярное произведение и преобразуем его:
.
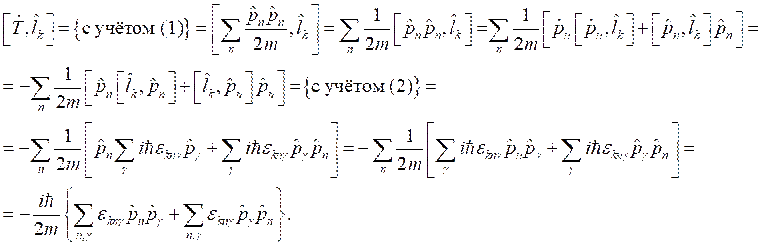Кроме этого выполняются следующие выражения:
.
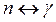С учётом этих выражений будет справедливо преобразование:
.
Получаем равенство:
.
Имеет место выражение: 
, а с учётом 
, имеем 
.
Извлекая квадратный корень из обеих частей этого равенства, получаем:
- что и требовалось показать.
Используя условие эрмитовости показать, что оператор проектирования является эрмитовым.
Решение.
Условие эрмитовости выглядит следующим образом:
.
По определению, оператор проектирования равен:
.
Проведём следующее преобразование:
.
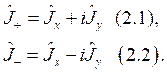Из последнего равенства видно, что оператор 
является эрмитовым, что и требовалось показать.
Показать, что если коммутатор операторов и равняется нулю, то имеет место следующий коммутатор: 
, где 
- операторная функция.
Решение.
Из того, что 
нужно показать выполнение вышеуказанного выражение.
Разложим операторную функцию в ряд Маклорена:
.
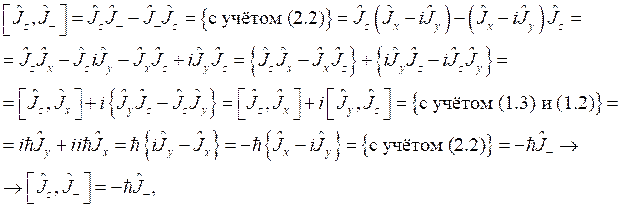Подставим эту операторную функцию в исходный коммутатор и преобразуем его:
.
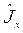Рассмотрим следующий коммутатор:
.
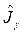Можно показать, что:
.
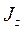Т.о. - что и требовалось показать.
Показать, что для любых кет-векторов 
и 
в пространстве Гильберта выполняется условие Шварца-Коши-Буняковского: 
, где знак 
возможен в случае коллинеарности 
и 
.
Подсказка: нужно рассмотреть произвольный вектор 
, где 
- комплексное число: 
.
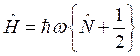Решение.
Вследствие выполнения равенства 
, справедливо следующее выражение:
.
Проведём непосредственное вычисление:
.
Учтём, что:
.
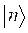Преобразуем выражение для 
с учётом формул для 
:
.
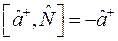Из выполнения неравенства, что 
, следует справедливость следующего неравенства:
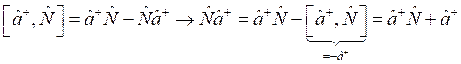
Преобразуем это выражение далее, умножая его на 
и учитывая равенство 
:
.
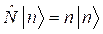Т.к. 
, то имеем следующее упрощение:
.
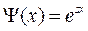Таким образом, получаем:
.
И последний шаг:
- что и требовалось показать.
Поможем написать любую работу на аналогичную тему