Используя спектральное разложение единичного оператора показать, что след матрицы произвольного оператора в дискретном базисе является инвариантом унитарного преобразования.
Решение.
Унитарное преобразование:
![]() (1).
(1).
Спектральное разложение единичного оператора:
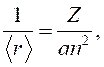 (2).
(2).
След матрицы оператора ![]() :
:
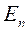 (3).
(3).
Требуется показать выполнение следующего равенства:
![]() .
.
Преобразуем правую часть этого часть:
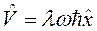
что и требовалось показать.
Показать, что след произведения двух квадратных матриц инвариантен относительно перестановки сомножителей.
Решение.
Требуется показать выполнение следующего равенства:
![]() .
.
Введём следующие обозначения:
![]() и
и ![]() .
.
По определению следа матрицы произвольного оператора:
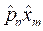
а матрица оператора ![]() с учётом нашего обозначения:
с учётом нашего обозначения:
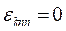
Производя подстановку матрицы оператора ![]() в определение следа, получаем:
в определение следа, получаем:
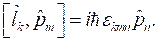
что и требовалось показать.
Показать, что среднее значение наблюдаемой L в состоянии, описываемом нормированным кет-вектором ![]() , может быть представлено в виде:
, может быть представлено в виде:
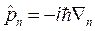 .
.
Решение.
По определению среднее значение наблюдаемой L:
![]() .
.
Если же состояние описывается нормированным кет-вектором, то:
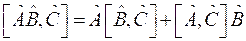 .
.
Таким образом, нужно показать следующее равенство:
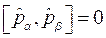 .
.
Рассмотрим отдельно представителя оператора ![]() :
:
![]() .
.
Сумма диагональных элементов матрицы оператора ![]() :
:
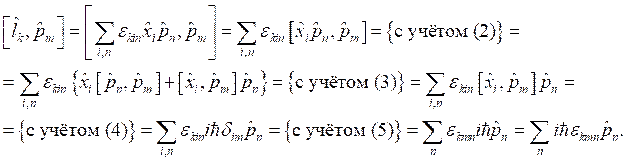 .
.
Сумма диагональных элементов произведения матриц операторов ![]() и
и ![]() :
:
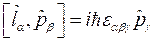
Таким образом: ![]() и
и ![]() , что и требовалось показать.
, что и требовалось показать.
Показать, что условие эрмитовости произвольного оператора ![]() в координатном представлении имеет вид:
в координатном представлении имеет вид:
![]() .
.
Решение.
Условие эрмитовости выглядит следующим образом:
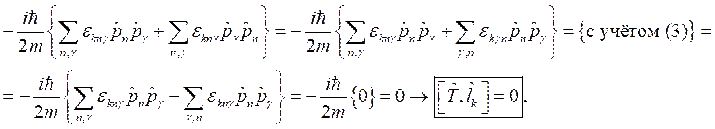 .
.
Для непрерывного спектра справедливы следующие выражения:
![]() ,
, ![]() ,
, ![]() .
.
Также учтём некоторые выражения:
![]() и
и ![]() .
.
Выполним преобразование следующего выражения с учётом выражений для непрерывного спектра:
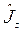
В результате преобразования получилось выражение:
![]() .
.
Аналогичным образом получается следующее выражение:
![]() .
.
Справедливо равенство: ![]() . С его учетом получаем:
. С его учетом получаем:
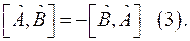
Таким образом, было показано, что:
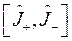 .
.
Используя условие эрмитовости произвольного оператора ![]() в координатном представлении
в координатном представлении ![]() показать, что оператор импульса в координатном представлении является эрмитовым на множестве квадратично интегрируемых функций
показать, что оператор импульса в координатном представлении является эрмитовым на множестве квадратично интегрируемых функций ![]() , т.е. функций, удовлетворяющих условиям:
, т.е. функций, удовлетворяющих условиям:
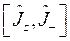 <
<![]() ,
, ![]() .
.
Решение.
Оператор импульса в координатном представлении имеет вид:
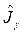 .
.
Распишем условие эрмитовости для оператора импульса в координатном представлении:
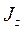
Первая часть интеграла равна нулю, так как ![]() . Рассмотрим вторую часть:
. Рассмотрим вторую часть:
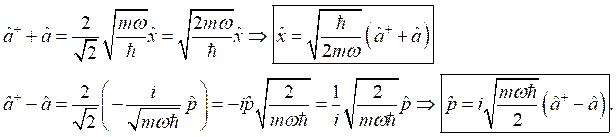
Таким образом, было показано выполнение равенства:
Показать, что среднее значение результатов измерения наблюдаемой L в произвольный момент времени t не зависит от способа описания временной эволюции квантовой системы, т.е. от выбора картины Гейзенберга или Шредингера.
Решение.
Условие унитарности оператора эволюции:
![]() .
.
Также необходимо учесть, что:
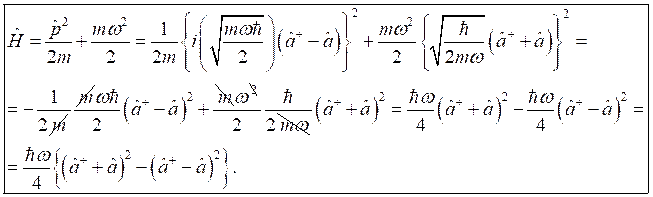 (1),
(1),
![]() (2) и
(2) и
![]() (3).
(3).
В картине Шредингера зависимость средних значений ![]() физических величин L от времени t возникает через временную зависимость векторов состояния
физических величин L от времени t возникает через временную зависимость векторов состояния ![]() , причём:
, причём: ![]() .
.
В картине Гейзенберга зависимость средних значений ![]() физических величин L от времени t определяется временной зависимостью операторов
физических величин L от времени t определяется временной зависимостью операторов ![]() , причём:
, причём: ![]() .
.
Таким образом, требуется проверить выполнение равенства:
![]() .
.
Преобразуем правую часть следующим образом:
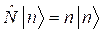
В итоге получили ![]() , что и требовалось показать.
, что и требовалось показать.
Доказать теорему Неймана: показать, что, если гамильтониан является функцией вещественного параметра λ, то среднее значение его производной по параметру λ в стационарном состоянии с энергией ![]() равняется производной этой энергии по параметру λ.
равняется производной этой энергии по параметру λ.
Решение.
Среднее значение находится по формуле:
![]() .
.
Для непрерывного спектра справедливы следующие выражения:
![]() ,
, ![]() ,
, ![]() (1).
(1).
Условие эрмитовости произвольного оператора ![]() в координатном представлении имеет вид:
в координатном представлении имеет вид:
![]() (2).
(2).
Уравнение на собственные функции и собственные значения для оператора Гамильтона в координатном представлении:
![]() .
.
Оператор Гамильтона удовлетворяет условию эрмитовости:
![]() (3).
(3).
Требуется показать выполнение следующего равенства:
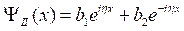 .
.
Распишем по формуле для среднего значения левую часть этого уравнения и преобразуем его:
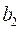
Далее выполним некоторое несложное преобразование:
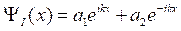 .
.
Вследствие справедливости равенства ![]() , упростим вышестоящее выражение:
, упростим вышестоящее выражение:
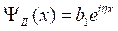
С учётом последних двух преобразований получаем:
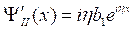
Теорема доказана.
Поможем написать любую работу на аналогичную тему

