Для решения этих задач необходимо решить стационарное уравнение Шредингера, которое в координатном представлении выглядит следующим образом:
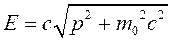 .
.
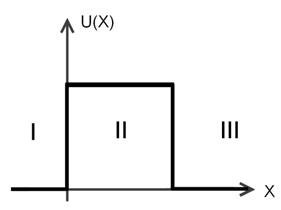
Поскольку здесь потенциальная энергия ![]() является разрывной функцией, это уравнение необходимо решить для каждой из областей в отдельности. Решениями будут функции, описывающие состояние частицы в этих областях, которые обозначим через
является разрывной функцией, это уравнение необходимо решить для каждой из областей в отдельности. Решениями будут функции, описывающие состояние частицы в этих областях, которые обозначим через ![]() . Для них в соответствии со свойством непрерывности Ψ-функции и её первой производной Ψ' по координате
. Для них в соответствии со свойством непрерывности Ψ-функции и её первой производной Ψ' по координате ![]() на границе области, где происходит конечный скачок функции
на границе области, где происходит конечный скачок функции ![]() , напишем следующие граничные условия в случае с тремя областями:
, напишем следующие граничные условия в случае с тремя областями:
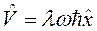 и
и 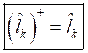 , где
, где ![]() - длина барьера или потенциальной ямы.
- длина барьера или потенциальной ямы.
3.1. Частица с массой ![]() находится в однородной прямоугольной потенциальной яме конечной глубины, где потенциальная энергия имеет вид:
находится в однородной прямоугольной потенциальной яме конечной глубины, где потенциальная энергия имеет вид:
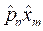
Показать, что при условии ![]() её энергетический спектр дискретный.
её энергетический спектр дискретный.
Решение.
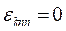
В нашем случае стационарное уравнение Шредингера перепишется следующим образом:
Для областей I и III: 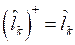 ;
;
Для области II: 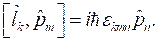 .
.
Решением дифференциального уравнения (1) является волновая функция ![]() . Подставляя это решение в (1) получаем:
. Подставляя это решение в (1) получаем:
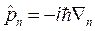 ,
,
а значит для областей I и III волновая функция примет следующий вид:
 .
.
Решением дифференциального уравнения (2) является волновая функция ![]() . Подставляя это решение в (2) получаем:
. Подставляя это решение в (2) получаем:
 ,
,
а значит для области II волновая функция примет следующий вид:
![]() .
.
Так же, это решение представимо в виде:
![]()
Решения уравнения (1) содержат экспоненты с вещественными показателями, которые неограниченно возрастают, когда ![]() стремится к бесконечности (
стремится к бесконечности (![]() ), причём волновая функция должна быть конечной при любых значениях
), причём волновая функция должна быть конечной при любых значениях ![]() , поэтому необходимо принять константы
, поэтому необходимо принять константы ![]() и
и ![]() равными нулю. Вследствие этого получим:
равными нулю. Вследствие этого получим:
I: ![]() , и
, и ![]() ,
,
II: ![]() , и
, и ![]() ,
,
III: ![]() , и
, и ![]() .
.
Учитывая граничные условия, перепишем эти уравнения в следующем виде:
 и
и  .
.
Умножим (1) уравнение на ![]() и вычтем из него (2), а уравнение (3) умножим на
и вычтем из него (2), а уравнение (3) умножим на ![]() и вычтем из него (4):
и вычтем из него (4):
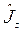 и
и 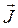 Выразим из (5)
Выразим из (5) ![]() и подставим его в (6):
и подставим его в (6):
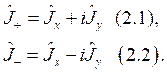 .
.
Подставим выражения для ![]() и для
и для ![]() в формулу для тангенса и преобразуем её с учётом того, что
в формулу для тангенса и преобразуем её с учётом того, что ![]() :
:
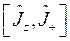
Так как ![]() , то выражение, стоящее в правой части близко к нулю и справедливо следующее преобразование:
, то выражение, стоящее в правой части близко к нулю и справедливо следующее преобразование:
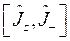 .
.
Таким образом, энергетический спектр данной частицы дискретный и пропорционален ![]() .
.
Найти значение энергии частицы с массой ![]() , находящейся в основном состоянии и обладающей потенциальной энергией
, находящейся в основном состоянии и обладающей потенциальной энергией 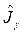 , зная вид собственной функции, которая описывает это состояние.
, зная вид собственной функции, которая описывает это состояние.
Подсказка: собственную функцию взять в следующем виде: ![]() (1).
(1).
Решение.
Справедливо следующее свойство равенства:
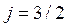 (2).
(2).
Перепишем стационарное уравнение Шредингера следующим образом:
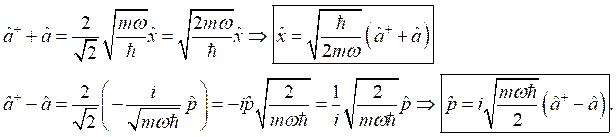 (3).
(3).
Возьмём вторую производную от Ψ-функции (1):
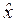
Далее подставим выражения для ![]() ,
, ![]() и
и ![]() в уравнение (3) и проводим некоторые преобразования:
в уравнение (3) и проводим некоторые преобразования:
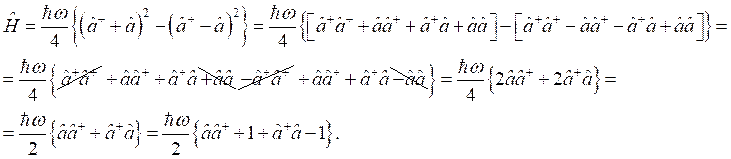
По свойству (2) получим некоторое равенство, из которого выразим энергию:
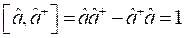 , что и требовалось найти.
, что и требовалось найти.
Частица находится в бесконечно глубокой потенциальной яме шириной ![]() . Определить отношение вероятностей обнаружения частицы в середине ямы и на расстоянии
. Определить отношение вероятностей обнаружения частицы в середине ямы и на расстоянии ![]() от края ямы. Вычисления провести для первого, второго и третьего стационарных состояний.
от края ямы. Вычисления провести для первого, второго и третьего стационарных состояний.
Решение.
Частица с массой ![]() и энергией
и энергией ![]() падает на прямоугольную потенциальную ступень:
падает на прямоугольную потенциальную ступень:
а) определить коэффициенты отражения и прозрачности для случая, когда ![]() ;
;
б) определить коэффициент отражения для случая, когда ![]() .
.
Решение.
а) Рассмотрим случай, когда ![]() , где требуется найти коэффициенты отражения и прозрачности, которые определяются по формулам соответственно:
, где требуется найти коэффициенты отражения и прозрачности, которые определяются по формулам соответственно:
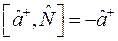 и
и ![]() .
.
В этом случае стационарное уравнение Шредингера для областей I и II перепишется в следующем виде:
I: 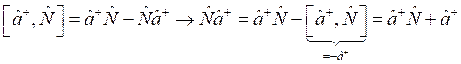 ,
,
II: 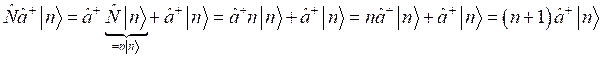 .
.
Решением дифференциального уравнения (1) является волновая функция ![]() . Подставляя это решение в (1) получаем:
. Подставляя это решение в (1) получаем:
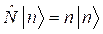 ,
,
а значит для области I волновая функция примет следующий вид:
![]() .
.
Решением дифференциального уравнения (2) является волновая функция ![]() . Подставляя это решение в (2) получаем:
. Подставляя это решение в (2) получаем:
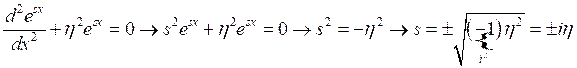 ,
,
а значит для области II волновая функция примет следующий вид:
![]() .
.
Так как в области II присутствует только волна, прошедшая через барьер и распространяющаяся в положительном направлении оси ОХ, то необходимо положить равным нулю коэффициент ![]() . Вследствие этого получим:
. Вследствие этого получим:
I: ![]() и
и ![]()
II: ![]() и
и ![]() .
.
С учётом граничных условий получим систему коэффициентов:
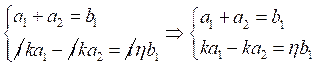 .
.
Отсюда найдём отношение коэффициентов ![]() и
и ![]() :
:
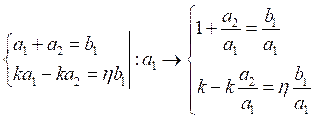 .
.
Подставляем ![]() во второе уравнение и находим
во второе уравнение и находим ![]() :
:
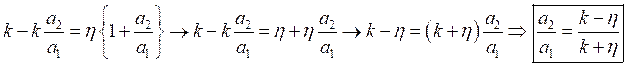 .
.
Находим коэффициент отражения: 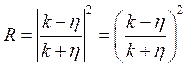 , а коэффициент прозрачности:
, а коэффициент прозрачности:
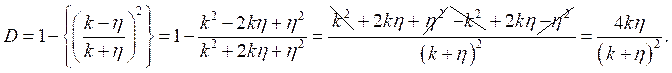
Таким образом: 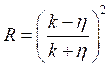 и
и 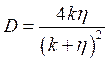 , где
, где 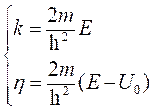 - что и требовалось найти.
- что и требовалось найти.
б) Рассмотрим случай, когда ![]() , где требуется найти коэффициент отражения, который определяется по формуле:
, где требуется найти коэффициент отражения, который определяется по формуле:
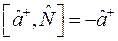 .
.
В этом случае стационарное уравнение Шредингера для областей I и II перепишется в следующем виде:
I: 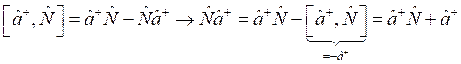 ,
,
II: 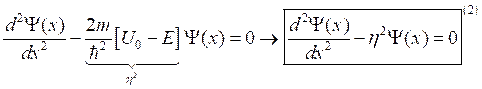 .
.
Решением дифференциального уравнения (1) является волновая функция ![]() . Подставляя это решение в (1) получаем:
. Подставляя это решение в (1) получаем:
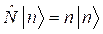 ,
,
а значит для области I волновая функция примет следующий вид:
![]() .
.
Решением дифференциального уравнения (2) является волновая функция ![]() . Подставляя это решение в (2) получаем:
. Подставляя это решение в (2) получаем:
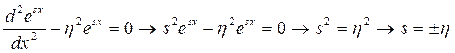 ,
,
а значит для области II волновая функция примет следующий вид:
![]() .
.
Решение уравнения (2) содержит экспоненты с вещественными показателями, которые неограниченно возрастают, когда ![]() стремится к бесконечности (
стремится к бесконечности (![]() ), причём волновая функция должна быть конечной при любых значениях
), причём волновая функция должна быть конечной при любых значениях ![]() , поэтому необходимо принять константу
, поэтому необходимо принять константу ![]() равную нулю. Вследствие этого получим:
равную нулю. Вследствие этого получим:
I: ![]() и
и ![]()
II: ![]() и
и ![]()
С учётом граничных условий получим систему коэффициентов:
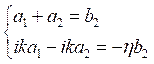 .
.
Отсюда найдём отношение коэффициентов ![]() и
и ![]() :
:
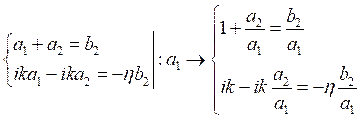
Подставляем ![]() во второе уравнение и находим
во второе уравнение и находим ![]() :
:
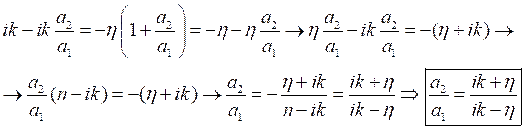
Таким образом, получили: 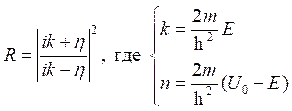 - что и требовалось найти.
- что и требовалось найти.
Электрон с энергией ![]() падает на потенциальный барьер, высота которого
падает на потенциальный барьер, высота которого ![]() , а ширина - 5Ǻ. Определить коэффициент прозрачности барьера.
, а ширина - 5Ǻ. Определить коэффициент прозрачности барьера.
Решение.
В этом случае полная энергия электрона больше, чем высота барьера, значит необходимо рассматривать случай, когда ![]() . Тогда стационарное уравнение Шредингера перепишется следующим образом:
. Тогда стационарное уравнение Шредингера перепишется следующим образом:
Для областей I и III: 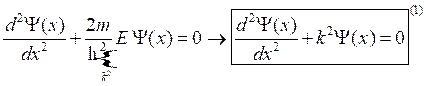 ;
;
Для области II: 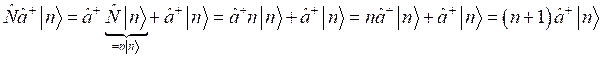 .
.
Решением дифференциального уравнения (1) является волновая функция ![]() . Подставляя это решение в (1) получаем:
. Подставляя это решение в (1) получаем:
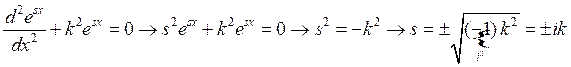 ,
,
а значит для областей I и III волновая функция примет следующий вид:
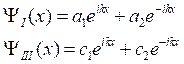 .
.
Решением дифференциального уравнения (2) является волновая функция ![]() . Подставляя это решение в (2) получаем:
. Подставляя это решение в (2) получаем:
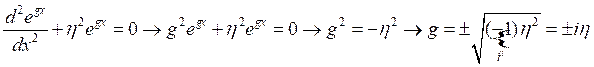 ,
,
а значит для области II волновая функция примет следующий вид: ![]() .
.
Так как в области III присутствует только волна, прошедшая через барьер и распространяющаяся в положительном направлении оси ОХ, то необходимо положить равным нулю коэффициент ![]() . Вследствие этого получим:
. Вследствие этого получим:
I: ![]() и
и ![]()
II: ![]() и
и ![]()
III: ![]() и
и ![]()
С учётом граничных условий получим систему коэффициентов:
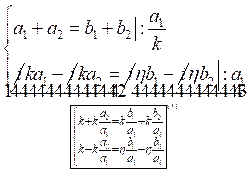 и
и 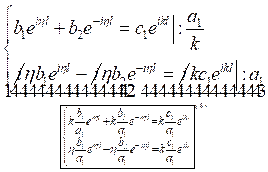 .
.
Введём некоторые обозначения: 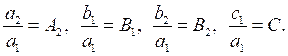
Перепишем системы (3) и (4) с учётом переобозначения:
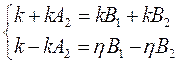 и
и 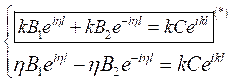 .
.
Коэффициент прозрачности определяется формулой:
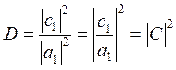 .
.
Для нахождения коэффициента прозрачности проведём некоторые преобразования:
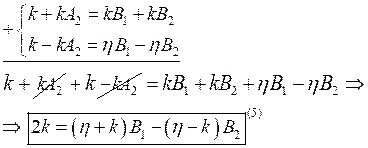 и
и 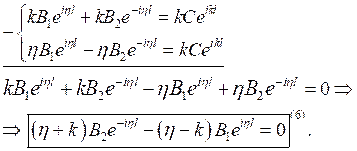
Из уравнения (6) выразим коэффициент ![]() :
:
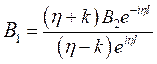 ,
,
а далее подставим его в уравнение (5):
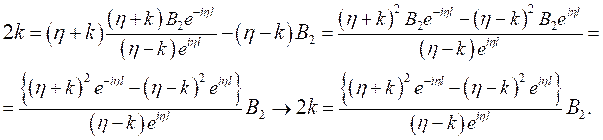
Выразим из полученного выражения коэффициент ![]() :
:
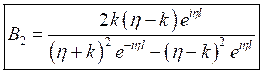 , а далее подставим это выражение в
, а далее подставим это выражение в ![]() :
:
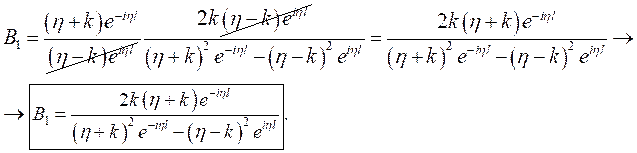
Подставим выражения для ![]() и
и ![]() в выражение
в выражение ![]() :
:
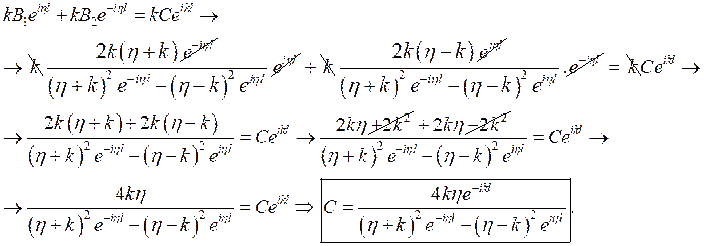
Таким образом, получили:
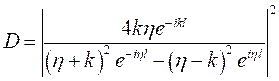 , где
, где 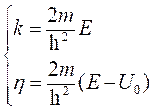 - что и требовалось найти.
- что и требовалось найти.
Интегрируя стационарное уравнение Шредингера в импульсном представлении, найти значение энергии ![]() и волновую функцию
и волновую функцию ![]() частицы, движущейся в однородном силовом поле, где потенциальная энергия меняется по закону
частицы, движущейся в однородном силовом поле, где потенциальная энергия меняется по закону ![]() .
.
Решение.
Поможем написать любую работу на аналогичную тему

