Показать, что нулевая энергия линейного гармонического осциллятора равная 
является его наименьшей энергией, совместимой с соотношением неопределённости.
Решение.
По определению гамильтониана линейного гармонического осциллятора:
.
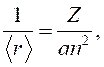Соотношение неопределённости Гейзенберга:
.
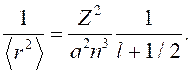Среднеквадратичное отклонение выражается формулой:
.
Требуется показать выполнение равенства:
.
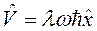Усредним гамильтониан линейного гармонического осциллятора:
.
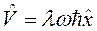Уравнение на собственные векторы и собственные значения оператора Гамильтона:
,
а тогда:
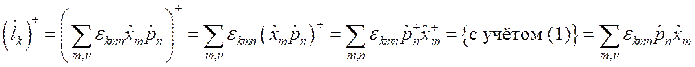(1).
Вернёмся к соотношению неопределённостей. Из формулы для среднеквадратичного отклонения следуют формулы:
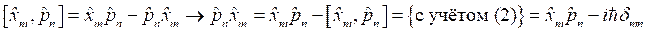
Чтобы использовать соотношение неопределённостей требуется доказать равенство нулю следующих величин: 
и 
. Если доказать, что величины 
и 
равны нулю, то и квадраты этих величин также будут равны нулю.
Операторы координаты и импульса в координатном представлении выглядят соответствующим образом:
и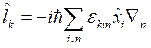 
.
,
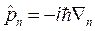т.к. интеграл от нечётной функции на симметричном отрезке равен нулю.
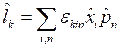
т.к. справедливо выражение: 
.
Таким образом, было доказано, что использование соотношения неопределённостей возможно и справедливы выражения:
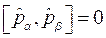откуда следует выполнения равенства для соотношения неопределённостей через величины 
и 
, т.е.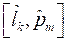 
.
Выразим отсюда величину для случая, когда 
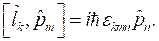, т.е. 
.
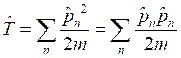Подставим в таком виде в выражение для энергии (1) и преобразуем последнее:
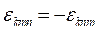(2).
Чтобы найти минимум энергии необходимо взять производную по и приравнять её к нулю:
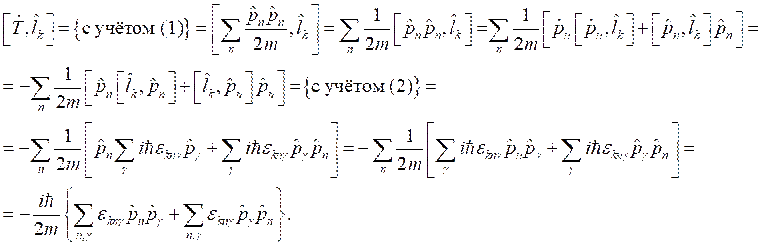, откуда выразим :
.
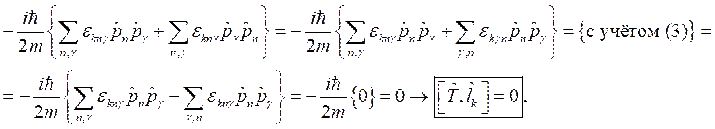Подставим это выражение в (2):
,
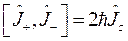что и требовалось показать.
Найти результат действия оператора числа частиц на нормированный собственный вектор.
Решение.
Действие операторов уничтожения и рождения на ортонормированный кет-вектор 
выражается формулами:
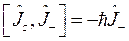
Требуется показать выполнение равенства:
.
Выполним несложные преобразования:
.
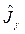Следовательно: , что и требовалось показать.
Показать, что коммутатор операторов уничтожения и рождения равен единичному оператору.
Решение.
Операторы рождения и уничтожения выражаются следующими формулами соответственно:
.
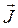Требуется показать, что
.
Выполним преобразования вышеуказанного коммутатора с учётом формул для 
и 
:
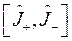
Из выполнения равенства: 
следует выполнение равенства 
, т.е.
, а значит:
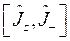, что и требовалось показать.
Показать, что оператор числа частиц является эрмитовым оператором.
Решение.
По определению оператора числа частиц:
.
Требуется доказать, что этот оператор является эрмитовым, то есть
.
Проведём несложные преобразования:
,
что и требовалось показать.
Выразить гамильтониан линейного осциллятора через оператор числа частиц.
Решение.
По определению оператора гамильтониана линейного гармонического осциллятора:
.
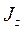Операторы рождения и уничтожения выражаются следующими формулами соответственно:
,
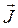откуда можно выразить операторы координаты и импульса:
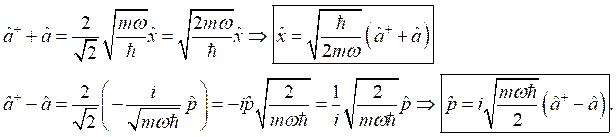
Подставим выражения для 
и 
в оператор Гамильтона и преобразуем получившееся выражение:
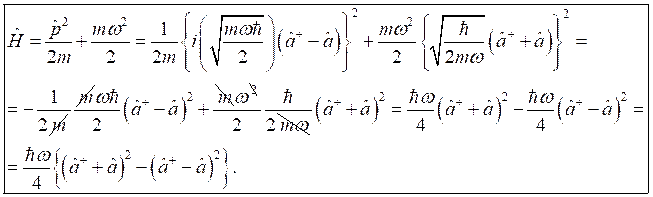(1)
Особое внимание необходимо уделить тому, что квадрат суммы и разности мы не можем расписать по обычным нам формулам, так как операции мы проводим не с числами, а с операторами, поэтому дальнейшие операции будут протекать по следующему способу:
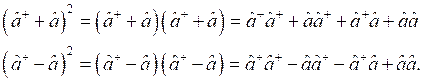
Подставим эти выражения в формулу (1) и преобразуем получившееся выражение:
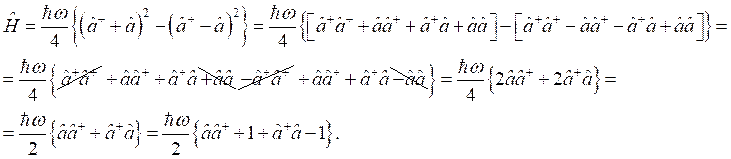
Далее учтём, что 
.
С учётом этого:
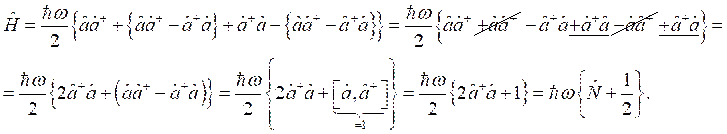
Таким образом, было показано, что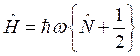 
, что и требовалось показать.
Показать, что результат действия оператора рождения на вектор 
является собственным вектором оператора числа частиц, принадлежащим собственному значению частиц 
.
Решение.
Уравнение на собственные значения и собственные кет-векторы оператора числа частиц:
,
а значит справедливо аналогичное выражение:
.
Также известно следующее коммутационное соотношение:
.
Требуется показать, что
.
Проведём некоторое преобразование вышеуказанного коммутатора:
.
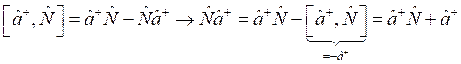Далее рассмотрим следующее преобразование:
.
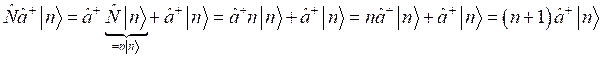Отсюда видно, что
,
а в силу равенства получается, что , что и требовалось показать.
Поможем написать любую работу на аналогичную тему