Момент количества движения.

Учитывая, что операторы координаты и импульса эрмитовы показать, что оператор декартовой компоненты орбитального момента тоже является эрмитовым.

Решение.

          По свойству эрмитовости для операторов координаты и импульса:

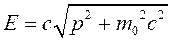 (1).

          Коммутатор операторов компоненты координаты и компоненты импульса:

 (2).

          Правило работы с дельта-символом Кронекера:

(3).

          Оператор декартовой компоненты орбитального момента:

,

а с учётом того, что , получаем: .

          Требуется показать выполнение следующего равенства:

.

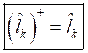          Произведём сопряжение оператора декартовой компоненты орбитального момента и далее преобразуем полученное выражение:

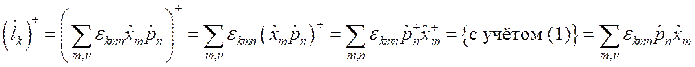 (4).

          Рассмотрим следующий коммутатор и его преобразование:

.

          Далее подставим выражение для  в выражение (4) и проведём преобразования:

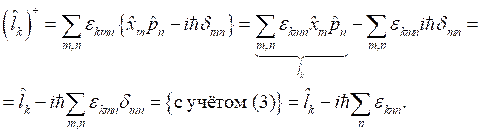
          Так как два индекса равны, то , что делает вычитаемое равным нулю, а значит:

, что и требовалось показать.

Показать, что коммутатор операторов компоненты орбитального момента и компоненты импульса определяется по формуле:

Решение.

          Оператор декартовой компоненты орбитального момента:

,

а с учётом того, что , получаем:

 (1).

          Правило раскрытия коммутатора:

 (2).

          Справедливы следующее коммутационные соотношения:

 (3),

 (4).

          Правило работы с дельта-символом Кронекера:

(5).

          Подставим выражение (1) в коммутатор  и раскроем его с дальнейшим преобразованием:

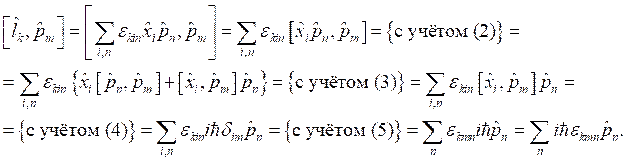
          Таким образом, получили искомое выражение:

Показать, что оператор кинетической энергии коммутирует с оператором декартовой компоненты орбитального момента.

Решение.

          Оператор кинетической энергии имеет следующий вид:

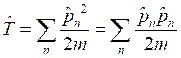 (1).

          Справедливо следующее равенство коммутаторов:

          Коммутатор операторов компоненты орбитального момента и компоненты импульса (2).

          Справедливо правило смены индексов для тензора Леви-Чевиты:

(3),

то есть при смене рядом стоящих индексов знак тензора меняется на противоположный.

          Требуется показать выполнение равенства нулю следующего коммутатора:

.

          Раскроем этот коммутатор «напрямую» и проведём некоторые преобразования:

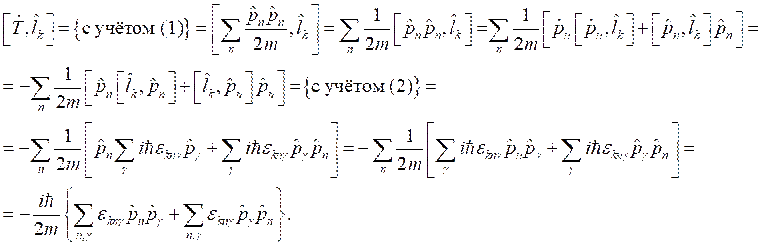
          Далее проведём смену индексов во второй сумме  и далее совершим преобразования:

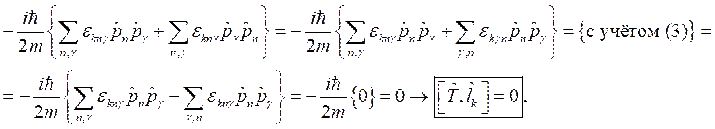
что и требовалось показать.

 Показать, что операторы повышения и понижения удовлетворяют правилам коммутации:

          а) ;

          б) ;

          в) .

Решение.

          Справедливы перестановочные соотношения для операторов проекций ,  и  момента количества движения :

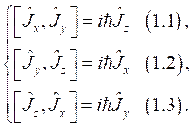
          Операторы повышения и понижения выглядят следующим образом соответственно:

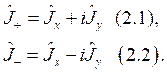
          По свойству коммутации операторов:

          а) Раскроем напрямую коммутатор  и проведём преобразования:

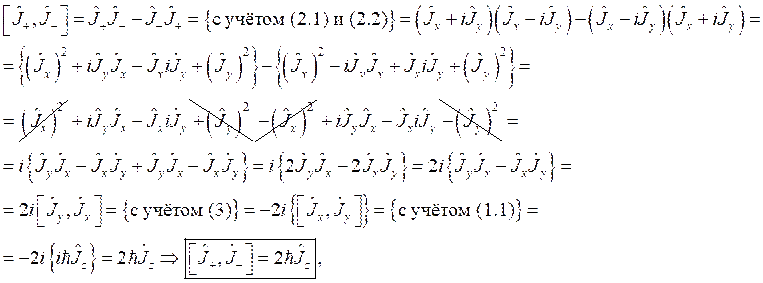
что и требовалось показать.

          б) Раскроем напрямую коммутатор  и проведём преобразования:

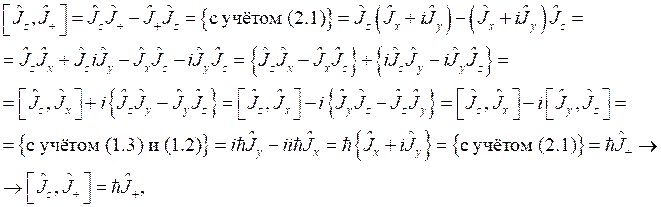
что и требовалось показать.

          в) Раскроем напрямую коммутатор  и проведём преобразования:

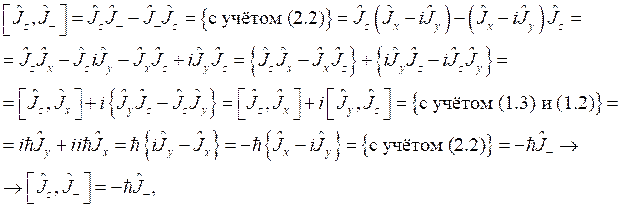
что и требовалось показать.

Найти матрицы операторов  и  полного момента количества движения в

- представлении для случая, когда внутреннее квантовое число.

Решение.

 Используя правило сложения моментов найти собственные значения скалярного произведения оператора спина двух электронов в состояниях, когда:

          а) их спины ориентированы в одну сторону;

          б) их спины ориентированы в разные стороны.

Решение.