Задание 2. Освободиться от иррациональности в знаменателе выражения.
a)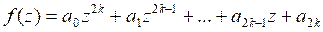 
Положим 
Тогда знаменатель является не чем иным, как элементарным симметрическим многочленом 
Попробуем подыскать множитель, после умножения на который знаменатель удастся выразить через степенные суммы 
вид
то знаменатель становиться рациональным выражением.
Для разыскания этого множителя используем формулы
Мы видим, что в обеих степенных суммах лишь последнее слагаемое (в правой части) не делится на 
Но очень легко скомбинировать эти степенные суммы так, чтобы меняющие нам последние слагаемые взаимно уничтожались. Для этого возведем сумму 
в квадрат
и вычтем из этого квадрата удвоенную сумму 
Мы получим:
откуда
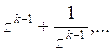
Пологая теперь в этой формуле 
мы найдем (используя указанные выше соотношения 
);
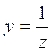
Остается умножить обе части полученного равенства на q и наша задача решена.
b)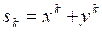 
.
Решение. Напишем выражение степенной суммы 
:
Здесь в правой части только последнее слагаемо 3
не делится на 
. Перенося его в левую часть, получаем:
откуда
Полагая здесь 
, 
находим:
=
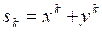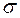
Таким образом видим, что если знаменатель дроби имеет вид 
, то после умножения числителя на выражение
-
В знаменателе получим выражение 
Теперь для освобождения от иррациональности достаточно использовать формулу
Надо умножить числитель и знаменатель на выражение
.
В результате мы получим:
=(-)
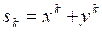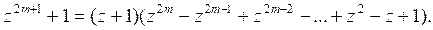
Поможем написать любую работу на аналогичную тему