Задание 3. Решить систему уравнений
a) Решение. Введем новые неизвестные 
, 
и обращаясь к таблице №1 приложения находим
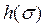
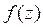
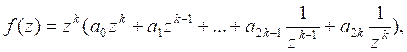
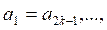
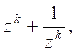
b) Решение.
Введем новые неизвестные , . Тогда система примет вид:
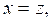
Для нахождения 
в первом уравнение системы воспользуемся теоремой Безу. Проверяя, являются ли
решением уравнения, находим, что 
=2 –корень. Следовательно, 
делится на на 
. Произведем деление, получаем, что
=()(
)
Следовательно, рассматриваемое кубическое уравнение распадается на два уравнения: линейное
=0,
которое дает уже известный корень =2,
и квадратное
которое дает еще два корня =2 и=-4
Возвращаясь к замене, получаем
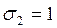или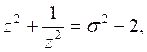 
Решая их, находим четыре решения первоначальной системы
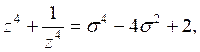
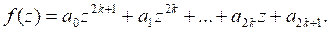
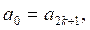
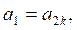
c) Решение. Освобождаясь от знаменателей и вводя новые неизвестные 
, получаем вспомогательную систему:
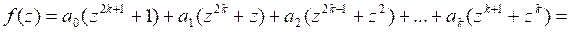
Сокращая первое уравнение на 
, что не приведет к потере решения, и подставляя вместо 
его значение из второго уравнения, получаем биквадратное уравнение 
. Отсюда находим четыре решения вспомогательной системы:
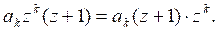
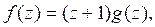
Каждая из них дает два решения исходной системы:
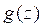
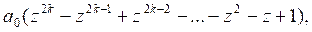
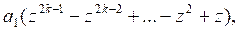
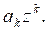
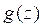
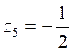
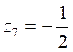
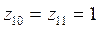
d) Решение: Полагая 
, 
приводим исходную систему к виду
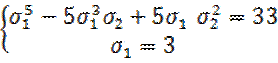
Отсюда для 
получаем квадратное уравнение
.
Из этого уравнения находим два значения для
и 
Таким образом, для первоначальных неизвестных получаем две системы уравнений
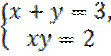
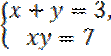
Решая эти системы, находим четыре решения первоначальной системы:
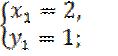
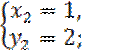
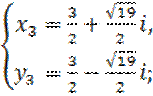
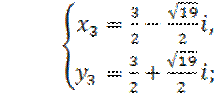
e) Решение: Полагая , приводим исходную систему к виду
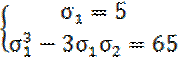
Ее решение 
Решение исходной системы:
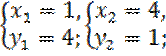
f) Решение: Пологая , приводим исходную систему к виду
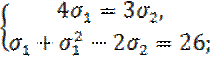
Исключая , получаем квадратное уравнение 
.
Отсюда находим два решения вспомогательной системы:
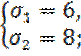
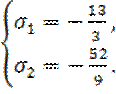
Каждое из них дает два решения исходной системы:
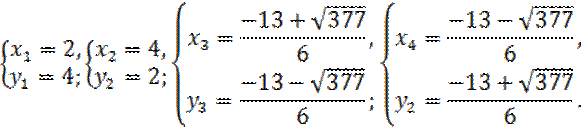
Поможем написать любую работу на аналогичную тему