Задание 4. Решить систему уравнений.
d) 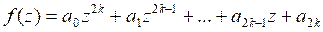
Решение. Введем новые неизвестные ![]() ,
,![]() ,
,![]() , положим
, положим
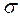
Или
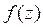
Из этой системы находим:
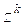
В развернутом виде эта система запишется так:
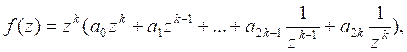
Для решения этой системы составляем согласно теореме кубическое уравнение
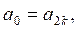
Левая часть уравнения разлагается на множители:
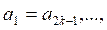 .
.
Следовательно, корнями этого уравнения являются числа
![]() ,
, 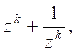
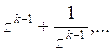 .
.
Поэтому исходная система шесть решений получающихся перестановками из решения
![]() ,
, 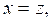
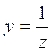 .
.
Задание 2. Решить систему уравнений
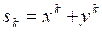
Положим ![]() Тогда система уравнений принимает симметрический вид
Тогда система уравнений принимает симметрический вид
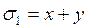
Такую систему мы уже решали (см. предыдущее задание). Там было найдено, что одним из решений является
![]() ,
, 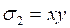
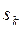 ,
,
а остальные пять решений получаются перестановками значений неизвестных ![]() Поэтому для первоначальных неизвестных мы получаем следующие шесть решений:
Поэтому для первоначальных неизвестных мы получаем следующие шесть решений:
1) ![]() ,
, 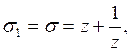
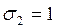 ;
;
2) ![]() ,
, 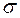
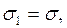 ;
;
3) 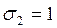 ,
, 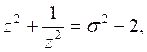
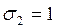 ;
;
4) 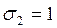 ,
, 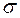
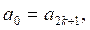 ;
;
5) 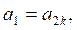 ,
, 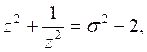
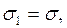 ;
;
6) 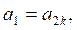 ,
, 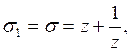
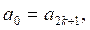 ;
;
Поможем написать любую работу на аналогичную тему

