Задание 5. Решить уравнение
a) Решение. Это возвратное уравнение имеет нечетную степень. Согласно теореме 3 его левая часть делится на z+1. Осуществляя деление, находим:
![]() = =
= =![]() .
.
Таким образом, уравнение разбивается на два:
z+1=0
![]() =0
=0
Первое из этих уравнений дает корень ![]() . Второе представляет собой возвратное уравнение четной степени. Преобразуем его левую часть:
. Второе представляет собой возвратное уравнение четной степени. Преобразуем его левую часть:
![]() =
=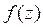
=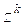
![]()
=![]()
Так как ![]() не является корнем исходного уравнения, то мы приходим к следующему уравнению относительно
не является корнем исходного уравнения, то мы приходим к следующему уравнению относительно ![]() :
:
![]()
Следовательно, мы имеем корень ![]() и еще четыре корня, которые легко найти, решая биквадратное уравнение
и еще четыре корня, которые легко найти, решая биквадратное уравнение
![]()
В результате находим пять значений для ![]() :
:
![]() ,
,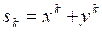
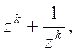
![]()
![]() .
.
Это означает, что для нахождения корней первоначального уравнения имеем пять уравнений:
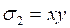
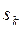 ,
,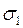 ,
,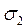 ,
,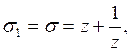 .
.
Решая их и учитывая найденный ранее найденный корень ![]() , получим одиннадцать корней исходного уравнения:
, получим одиннадцать корней исходного уравнения:
b) Решение. Это возвратное уравнение имеет четную степень. Согласно теореме его левая часть представима следующим образом:
![]() +9=
+9=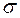
Так как ![]() не является корнем исходного уравнения, то мы приходим к кубическому уравнению относительно
не является корнем исходного уравнения, то мы приходим к кубическому уравнению относительно ![]() :
:
![]()
Левую часть легко разложить на множители:
![]()
(можно было также подбором найти корень ![]() и затем применить теорему Безу). Теперь легко находим три корня:
и затем применить теорему Безу). Теперь легко находим три корня:
![]() ,
, ![]()
Решая их, находим шесть корней первоначального уравнения:
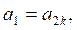
c) Решение. Имеем 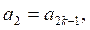
Получаем двучленное уравнение ![]() =0. Его корни:
=0. Его корни:
![]()
Для нахождения корней первоначального уравнения имеем четыре уравнения:
![]() ,
,![]() ,
, ![]() .
.
Решая их находим восемь корней первоначального уравнения:
![]() ,
, ![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
, 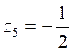 ,
, ![]() ,
,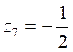 ,
, ![]() ,
,![]() .
.
Поможем написать любую работу на аналогичную тему

