Приложение 9 по методике преподавания - Симметрические многочлены в профильном обучении школьников

Задание 6. Решение. Для доказательства введем элементарные симметрические многочлены  и , тогда .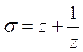

Так как , а по условию задачи , то 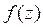, т.е.

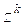
Применяя к полученному неравенству тоже рассуждения находим, что                      

.

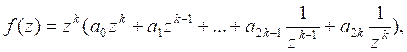Аналогично находим, что

.

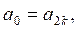Задание 7. Решение. Положим , . Тогда доказываемое неравенство примет вид

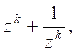
или . Мы должны доказать справедливость этого справедливость этого неравенства при  . Имеем:

Последнее выражение в самом деле не отрицательно так как , (по теореме см. выше).

Задание 8. Решение. Мы имеем:

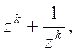
Задание 9.  Решение. Полагая здесь  получаем:

а это и есть доказываемое неравенство.