Теорема 3. Всякий возвратный многочлен ![]() четной степени 2k
представляется в виде f(z)=
четной степени 2k
представляется в виде f(z)=![]() , где
, где 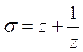 и
и ![]() - некоторый многочлен степени k от
- некоторый многочлен степени k от![]() .
.
Всякий возвратный многочлен f(z) нечетной степени делится на z+1, причем частное представляет собой возвратный многочлен четной степени.
Доказательство. 1) Рассмотрим сначала многочлен ![]() четной степени 2k. Вынося в этом многочлене за скобки
четной степени 2k. Вынося в этом многочлене за скобки ![]() , получим:
, получим:
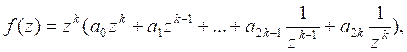
или принимая во внимание равенство ![]()
![]()
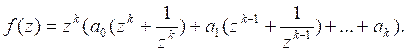
Докажем, что двучлены 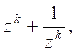
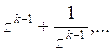 можно выразить через
можно выразить через 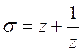 . Положим
. Положим ![]()
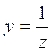 , то степенная сумма
, то степенная сумма ![]() превратится в выражение
превратится в выражение 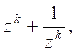 элементарный симметрический многочлен
элементарный симметрический многочлен ![]() - в
- в 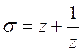 , а элементарный симметрический многочлен
, а элементарный симметрический многочлен ![]() примет значение 1. Поэтому, подставляя в выражение степенной суммы
примет значение 1. Поэтому, подставляя в выражение степенной суммы ![]() через
через ![]() и
и ![]() значения
значения 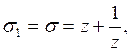
![]() , мы получим искомое выражение двучлена
, мы получим искомое выражение двучлена 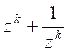 через
через ![]() .
.
Практически для этого удобно использовать формулы из таб. 1 Приложения 1. Пологая в этих формулах ![]()
![]() , получаем:
, получаем:
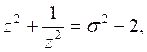
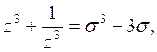
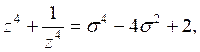
………………………………………………………
2)Рассмотрим теперь случай возвратного многочлена нечетной степени 2k+1:
![]()
Так как этот многочлен является возвратным, т.е. выполнены равенства ![]()
![]()
![]() …,
…,
то его можно записать в следующем виде:
![]()
![]()
В каждом двучлене, стоящем в скобках, можно выделить множитель z+1, воспользовавшись следующим хорошо известным равенством:
![]()
Мы получим:
![]()
![]()
……………………………………………………………………………….
![]()
Складывая полученные выражения почленно и вынося в правой части множитель z+1 мы получим:
![]()
где ![]() - многочлен, являющийся суммой следующих многочленов:
- многочлен, являющийся суммой следующих многочленов:
![]()
![]()
………………………….
![]()
Непосредственно видно, что во всех этих многочленах коэффициенты, равноудаленные от концов, совпадают, и потому их сумма ![]() является возвратным многочленом (четной степени 2k). Теорема доказана.
является возвратным многочленом (четной степени 2k). Теорема доказана.
Поможем написать любую работу на аналогичную тему

