Показателем тесноты связи, устанавливаемой между результативными и двумя или более факторными признаками, является совокупный коэффициент множественной корреляции Ryx1x2. В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле:
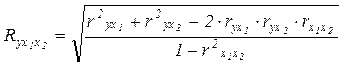 (10)
(10)
где rух1, rух2, rх1х2 – линейные (парные) коэффициенты корреляции, применяемые для измерения тесноты между рассматриваемыми факторами.
Совокупный коэффициент множественной корреляции измеряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах - 1 до +1. Чем меньше наблюдаемые значения изучаемого показателя отклоняются от линии множественной регрессии, тем корреляционная связь является более интенсивной, а, следовательно, значение R ближе к единице.
Совокупным коэффициентом множественной детерминации называется величина R2, которая показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Значение совокупного коэффициента множественной детерминации находится в пределах от 0 до 1. Поэтому, чем ближе R2 к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.
Поможем написать любую работу на аналогичную тему

