Однако показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов. Поэтому только после проверки адекватности уравнения оно может быть пригодно, например, для выявления резервов повышения производительности труда.
Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F-критерия Фишера. Применение же в этих целях множественного коэффициента корреляции недопустимо ввиду того, что многофакторный регрессионный анализ оперирует случайными наблюдениями, но не обязательно распределенными по многомерному нормальному закону (этому закону должны подчиняться отклонения фактических значений функции от расчетных). Совокупный коэффициент множественной детерминации определяет только качество выравнивания по уравнению регрессии.
Проверку значимости уравнения регрессии производят на основе вычисления F-критерия Фишера:
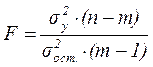(11)
где m – число параметров в уравнении регрессии; п – объем выборки; σост. – среднее квадратическое отклонение результативного признака у от выровненных значений ŷ.
(12)
Полученное значение критерия Fрасч. сравнивают с критическим (табличным) для принятого уровня значимости 0,05 или 0,01 и чисел степеней свободы v1 = m-1, v2 = n-m. Если оно окажется больше соответствующего табличного значения, то данное уравнение регрессии статистически значимо, то есть доля вариации, обусловленная регрессией, намного превышает случайную ошибку.
Считается, что уравнение регрессии пригодно для практического использования, если Fрасч. > Fтабл. не менее, чем в четыре раза.
Для оценки значимости коэффициентов регрессии (а1…i) при линейной зависимости у от двух факторов (х1 и х2) используют t-критерий Стьюдента при n-m-1 степенях свободы:
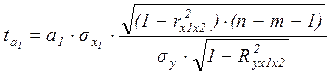(13)
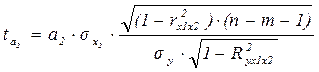(14)
Проверку адекватности уравнения регрессии можно также провести на основе расчета существенности совокупного коэффициента корреляции, сравнив его затем с критической величиной, взятой из таблицы Стьюдента. При этом используется следующая формула:
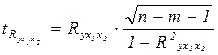(15)
Значение 
берется по модулю. Если табличное значение t-критерия
при 5%-ом уровне значимости меньше полученного в ходе эксперимента, то построенную модель признают пригодной для практического применения.
В свою очередь, если результаты проверки адекватности привели к отрицательным результатам, то в этом случае в исследовании, скорее всего, были либо неверно определены факторы, оказывающие влияние на исследуемый процесс, либо неправильно выбрана сама модель исследования.
А если результаты проверки адекватности привели к положительным результатам, то далее следует проверить эффективность ее применения на малой выборке, и, в случае получения положительных результатов, распространить на всю генеральную совокупность.
Значения оцениваемых a1,a2, Ryx1x2 берутся по модулю.
Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.
Оценку значимости коэффициентов регрессии с помощью t-критерия используют для завершения отбора существенных факторов в процессе многошагового регрессионного анализа. Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем уравнение регрессии строится без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов. В некоторых случаях расчетное значение tрасч находится вблизи tтабл., поэтому с точки зрения содержательности модели такой фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов.
Последовательный отсев несущественных факторов рассмотренным выше приемом (или последовательным включением новых факторов) составляет основу многошагового регрессионного анализа.
Поможем написать любую работу на аналогичную тему