При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значений х. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений ei и значения xi будут коррелированы.
Значения xi и ei ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
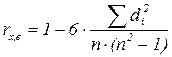(1)
где di – разность между рангами xi и еi, i = 1,2, ..., n; n – число наблюдений.
Если коэффициент корреляции rх,е для генеральной совокупности равен нулю, то статистика
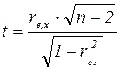(2)
имеет распределение Стьюдента с числом степеней свободы v = n - 2.
Далее, если наблюдаемое значение t-статистики превышает табличное, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции rх,е, а, следовательно, и об отсутствии гетероскедастичности.
Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощью t-статистики для каждой из них отдельно.
Тест Парка
Парк предложил критерий определения гетероскедастичности, дополняющий графический метод некоторыми формальными зависимостями.
Предполагается, что дисперсия
(3)
является функцией i-o значения xi объясняющей переменной. Парк предложил следующую функциональную зависимость:
(4)
Прологарифмировав, получим:
(5)
Так как дисперсии 
обычно неизвестны, то их заменяют оценками квадратов отклонений 
.
Критерий Парка включает следующие этапы:
1. Строится уравнение регрессии уi =b0 +b1·xi +ei.
2. Для каждого наблюдения определяются 
.
3. Строится регрессия 
, где 
.
4. Проверяется статистическая значимость коэффициента β уравнения на основе t-статистики.
Если коэффициент β статистически значим, то это означает наличие связи между ln(ei2) и ln(xi), то есть гетероскедастичности в статистических данных.
Поможем написать любую работу на аналогичную тему